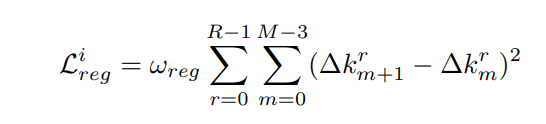Deep Retinex Net

主要贡献

• 建立了一个 采集与真实场景的 含有成对的低光照/正常光照的大尺度数据集（包含了合成和非合成的图像）
• 提出了一个基于retinex理论的图像分解的深度神经网络模型。这个模型是端到端训练的。
• 提出了用于学习图像分解模型的结构加权总变分损失。能够较好的平滑光照图同时保留原本的结构

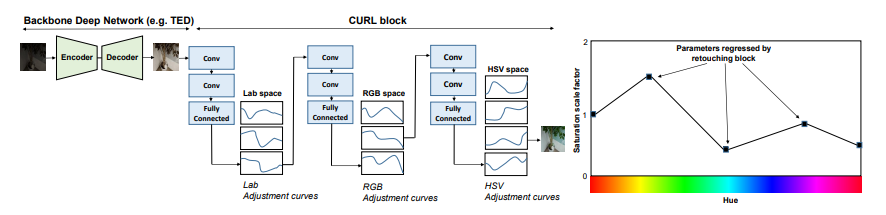
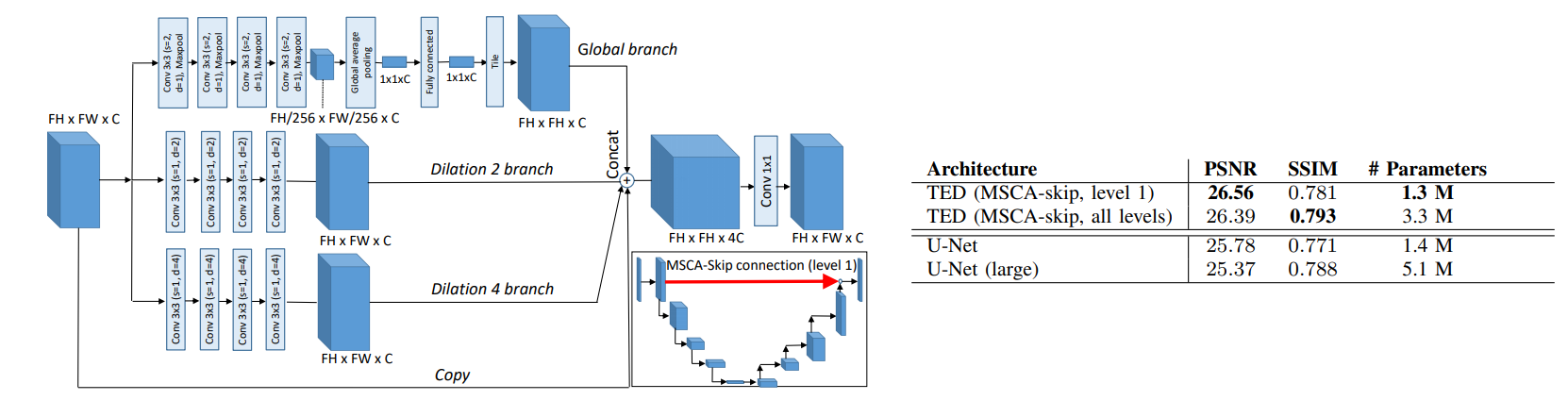
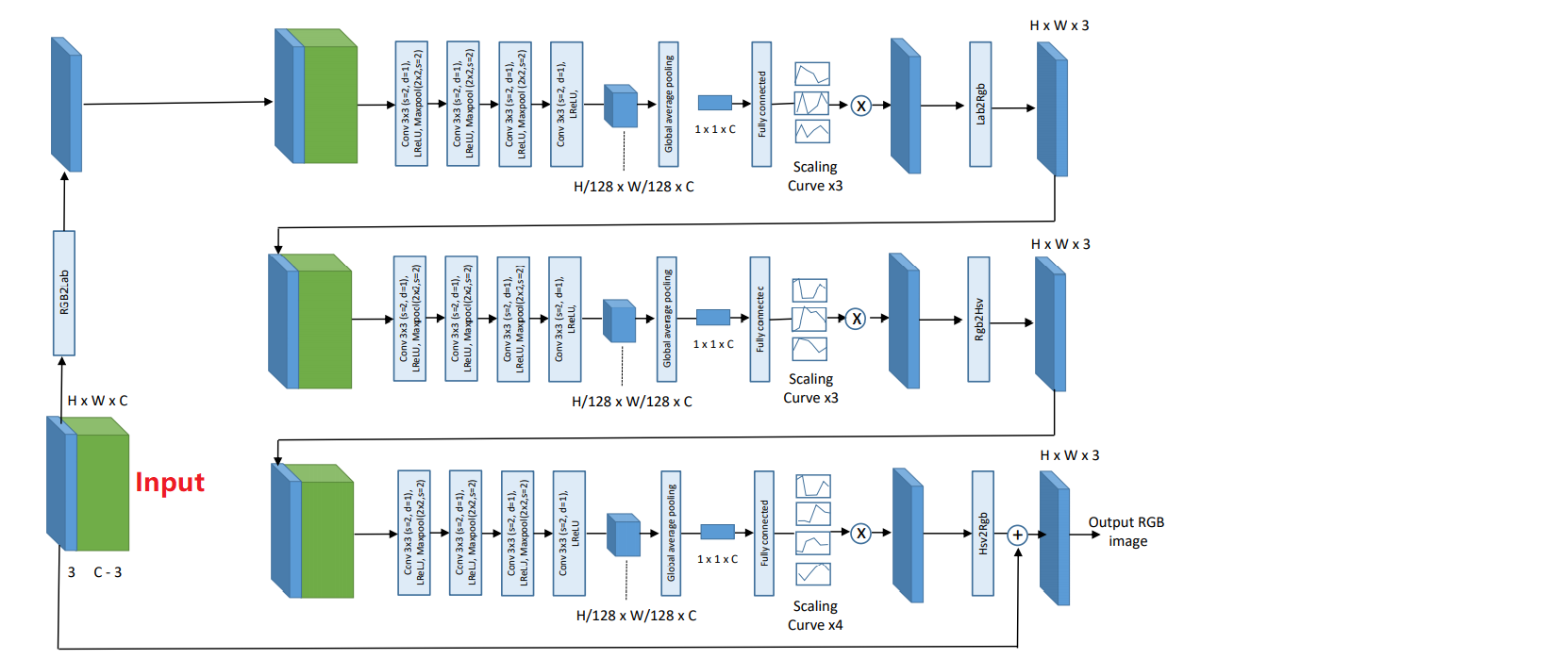
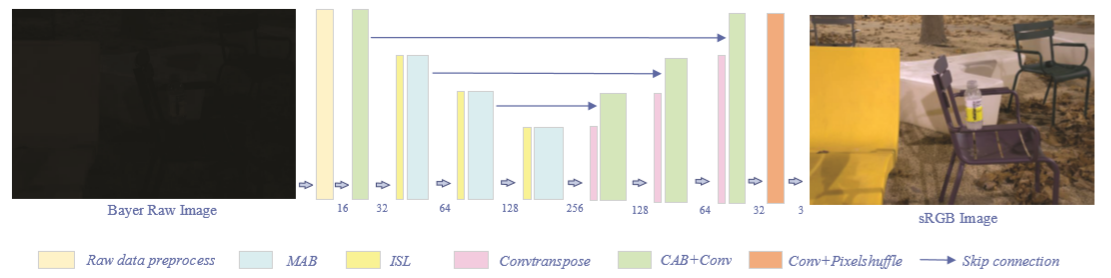
网络结构

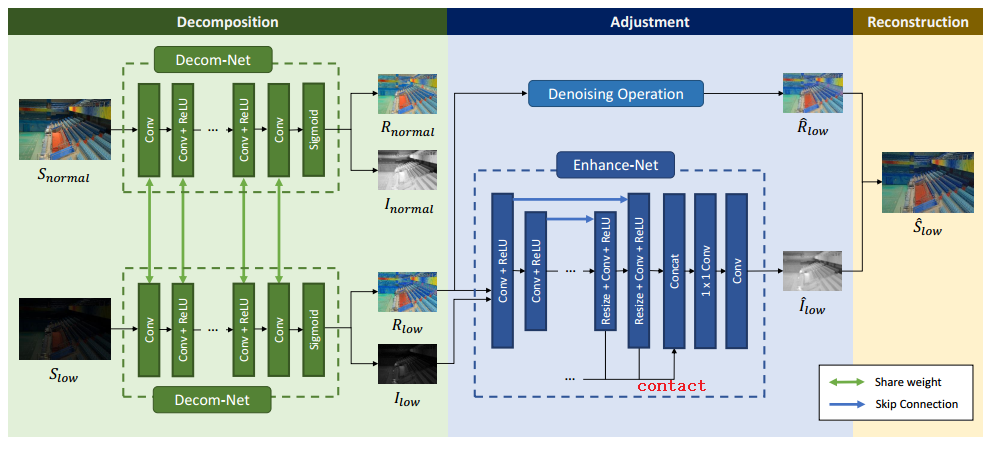
​ 可以看出，整个模型由序列的两部分组成，图像分解，和 去噪以及亮度多尺度调整

数据驱动的图像分解 Decom-Net

​ 这一部分将输入图像 S 分解为光照估计 I 和反射分量 R。一种分解反射和光照的方法是使用人工约束条件。然而根据retinex模型的那个式子很难实现，作者使用数据驱动的方式构建一个 Decom-Net来完成。这个网络的特点是损失函数的设计。由上图看出DecomNet的训练不需要低光照图的R和L来直接构建损失，而是通过以下几个约束条件来间接构建损失函数。

• 低光照图的反射率图和正常光照的反射率图应该尽可能一样： \[ \mathcal{L}_{i r}=\left\|R_{l o w}-R_{n o r m a l}\right\|_{1} \]

• 应该可以根据R, I 还原重建出 I 对应的 S图 。假设Sn Sl分别为输入正常光照和低光照图像， Il In为分解产生的高低光照图 Rn Rl 为分解产生的对应的反射率。约束1可知Rn应该尽可能接近Rl。 约束2的意思则是： 使用Rn Il 可以还原出Sl 使用Rn In可以还原出Sn 使用Rl Il可以还原出Sl 使用Rl In可以还原出Sn 。 R*I 即根据Retinex理论重建的过程，而-则来度量还原的程度。

\[ \mathcal{L}_{\text {recon}}=\sum_{i=l o w, n o r m a l} \sum_{j=l o w, n o r m a l} \lambda_{i j}\left\|R_{i} \circ I_{j}-S_{j}\right\|_{1} \]

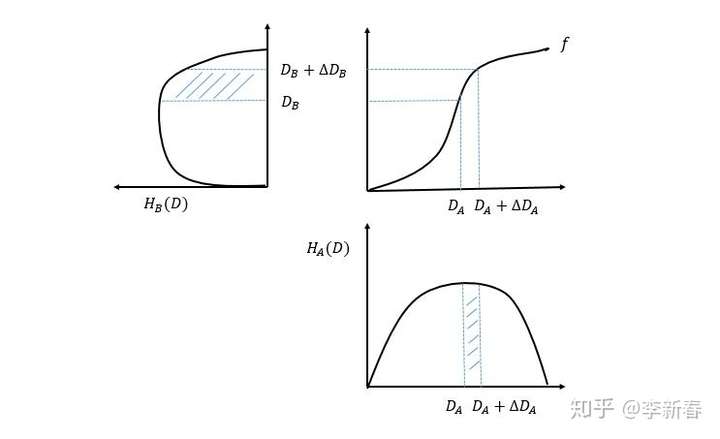
• 结构平滑损失。即分解产生的光照图应该尽可能的平滑，因为认为一张图上的光照在各个区域是一致的。全变分(TV)损失，最小化整张图的梯度，通常在图像重建中作为先验平滑图像。但是直接应用TV损失来约束平滑光照图会在 图像本身梯度较大的区域失效 （下图黑边）。这是由于不管区域是纹理细节还是强边界，光照梯度都是均匀减少的。因此原本的TV损失对图像的结构是盲目的，如果在图像边缘进行强烈的模糊虽然产生的光照图会平滑但是反射率图会产生黑边。如下图。因此根据对应位置的反射率对光照梯度加上权重。上式 \(\nabla I_{i}\) 表示微光图/正常光照图的梯度，一般的TV损失是直接对全图\(\nabla I\) 求和作为损失来优化平滑图像。这里相当于根据反射率图像的梯度给梯度加上了一个权值exp()。在反射率图本身梯度大的地方权值小，小的地方权值大。作者认为在物理结构存在梯度的地方光照应该不连续 ？？

\[ \mathcal{L}_{i s}=\sum_{i=l o w, n o r m a l}\left\|\nabla I_{i} \circ \exp \left(-\lambda_{g} \nabla R_{i}\right)\right\| \]

• 将上述三部分损失相加即为Decom-Net 采用的损失 \[ \mathcal{L}=\mathcal{L}_{\text {recon}}+\lambda_{i r} \mathcal{L}_{i r}+\lambda_{i s} \mathcal{L}_{i s} \] 作者还提到 关于LIME网络也在计算光照图像时考虑到图像原本的结构，但是本质和自己的不同....

For LIME, the total variation constraint is weighted by an initial illumination map, which is the maximum intensity of each pixel in R, G and B channels. Our structure-aware smoothness loss instead is weighted by reflectance. The static initial estimation used in LIME may not depict the image structure as well as reflectance does, since reflectance is assumed as the physical property of an image.

多尺度光照调节 adjustment

​ 这个adujust网络的结构类似于U-net 的编码解码结构。降采样块包含步长为2的卷积层，上采样块使用resize-convolution层，即先将特征图插值的方法上采样然后使用步长为1的卷积和激活。这一部分的损失即为调整过后的光照图和去噪过后的反射率图重建产生的图像和正常光照图像之间的l1损失。 ​ 可以看到，在这一部分还对反射率图进行了去噪处理，使用的时DMB3

数据集

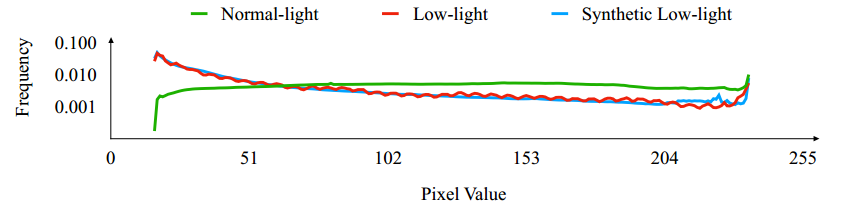
​ 作者提出了一套数据集，包含两部分：成对的合成数据和真实的低光照图。由于真实场景的图像采集正常光照和低光照时会产生错位，作者采用了三步法来矫正。 ​ 合成图像，作者分析了已有的真实低光照图像和真实的正常图像光照的YCbCr中Y的分量，统计Y分量的直方图，根据他们的规律来合成低光照图像。

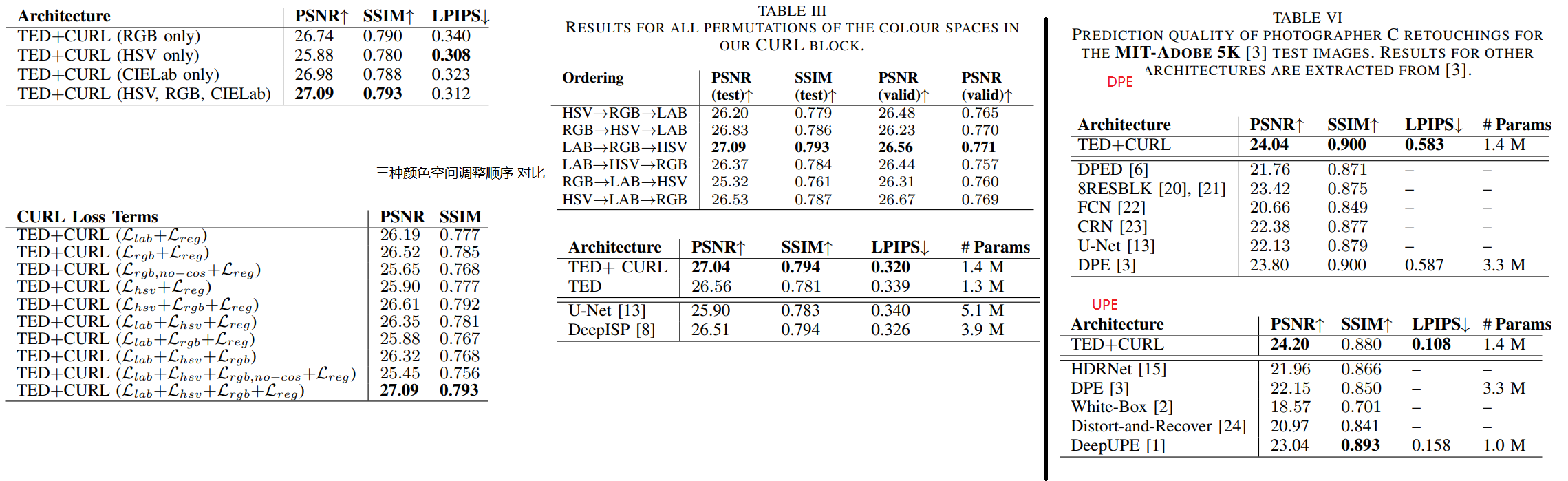
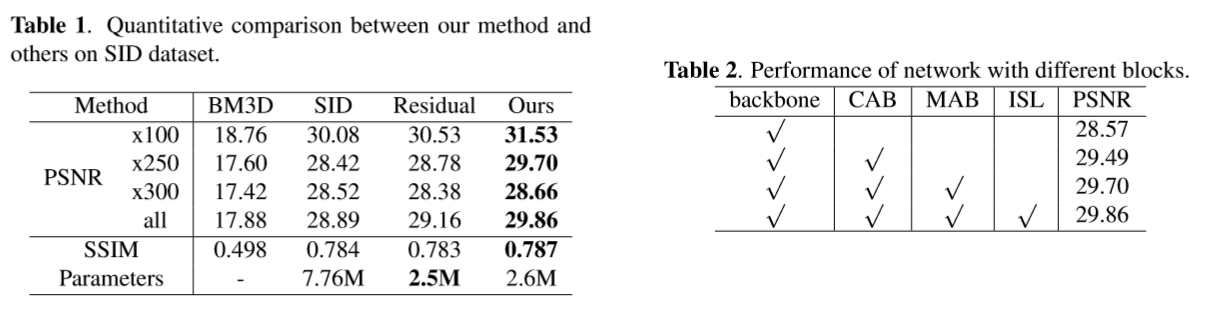
结果

​ 本论文作者并没有贴出指标的定量分析，只是贴了几幅图。图像分解的方法是否有效有待考虑.... ​ 定性分析：

1. 首先作者为了证明图像分解网络设计的有效性，贴出了和LIME分别对微光图和正常图像分解产生的R , I图，发现LIME在同一个图的低光和正常光图分解的R结果并不一致， 而R反应的应该是物体本身的折射率，在低/正常图下应该一样。

2. 同样的，在R图中 由于去掉了光照分量，应该不存在阴影，而LIME的R中存在明显的阴影，但是RetinexNet除了有噪 声外是没有阴影的 说明光照分量取出的比较彻底。

3. 文章所提的方法不会对局部区域过曝，主要是全局光照调节效果好

4. 得益于加权TV损失，相对于基于DeHz去雾方法 结果中没有黑边

5. 又对比了同样含有去噪方法的JED 网络，LIME(网络后去噪) 结果，发现Retinex的边缘细节得到较好的保留。

   

感觉这种方法处理的结果

CURL: Neural Curve Layers for Global Image Enhancement

主要贡献

• 基于多颜色空间的曲线调整块 CURL 神经修饰块。通过神经网络学习一条离散的点，代表一条曲线。使用该曲线分别在 Lab RGB 以及 HSV空间 对图像进行全局调整。
• 提出了多颜色空间损失函数 就是每个颜色空间调整完后的结果都有个损失函数约束
• 改进了U-NET的编解码结构，提出TED的backbone。降低参数量的同时提升了性能

主要内容

主要结构

主要流程从上图可以看出 首先使用一个编解码结构对输入图像处理，作者使用的是自己改进的TED结构做backbone。backbone输出一个特征图记为 F（多通道），取特征图 F 的前三通道为编解码器输出的RGB图像，后面的通道为特征。接着的CURL模块就是对这个RGB图做全局调整。首先将前三通道RGB图转为Lab格式，然后和剩余的特征图一起输入第一个块，输出得到一个向量（代表曲线），并使用这个曲线对Lab空间下的图调整后转为RGB格式 输入下一部分曲线调整模块。以此类推。

TED

TED的核心结构和UNET类似，右下角所示结构。和UNET的差别是，首先取消了UNET的每一层的跳跃连接，只保留了最高层的连接，并且这个连接作者称为 MSCA-skip 如图中红色的连线。MSCA结构是左边大图所示，有三个分支，最上面的分支是全局连接，有几个步长为2的卷积加最后一个全连接。中间分支是卷积率为2的分支，最下面是卷积率为4的分支。最后concat 1x1卷积压缩输出。输入输出特征图尺寸通道数一致。作者对比了他提出的这个TED 结构和 UNET的准确率参数量，可以看出参数量较少但是准确率还比较高。同时还看出只有第一层跨层连接参数量少很多但是效果不输全部都连接的情况。

另外，作者还讨论了两种输入模式，RGB-to-RGB, RAW-to-RGB 两种情况。对于RAW格式的输出，需要稍微欸修改backbone的编码结构，具体的就是使用 pixel-shuffle层将输入RAW格式 转化为 (H/r) (W/r) r^2 然后再输入bacnkbone的下采样路径，这样输出的尺寸是RGB的四分之一，再使用pixel shuffle的上采样方法获得和RGB输如一样大的特征图。RGB格式的输入就不使用 pixel shuffle操作了。RAW需要pixel-shuffle主要是因为RAW格式数据的特殊存储格式吧。

CURL模块

可以看出 前面 backbone输出的是一个 特征图 取特征图前3通道（蓝色部分为RGB图）曲线就是对这个进行全局调整的。神经网络的输出曲线是由全连接层产生，即离散的点。调整公式如下。 M代表输出点的个数，km代表第m个点的值，I 代表输入像素值，S代表输出的调整缩放因子。因此最终的调整结果为 S*I 这样的另一个巧妙之处在于，例如HSV通道，可以使用 hue 对 saturation 进行调整（色相至饱和度曲线），换句话说缩放因子用 通道hue 计算，但是用算出来的缩放因子对saturation 通道调整。

we arrange the neural curve layers in a particular sequence, adjusting firstly luminance and the a, b chrominance channels (using three curves respectively) in CIELab space. Afterwards, we adjust the red, green, blue channels (using three curves respectively) in RGB space. Lastly hue is scaled based on hue, saturation based on saturation, saturation based on hue, and value based on value (using four curves respectively) in HSV space

这个公式这么理解：

损失函数

上面的模块中涉及到 颜色空间的变换 作者使用的是 pytorch 可微分的变换实现。

为什么 要用乘积？ S V乘积相同但是 相反表示不同深浅的颜色，但是损失依然为0？所以为啥要乘积相等？

最后一个损失很明显是约束曲线 的斜率 不要有太大的突变 防止过拟合 即相邻点之间的直线的斜率差距不要太大。

实验

作者在三个数据集上验证了算法

• Samsung S7 90张训练 10张测试 10张验证 包含RAW/RGB图像对
• MIT-Adobe5k-DPE 5000张图，有专家调整的参考图 2250对训练图 500张测试 从训练集随机选择了500个做验证
• MIT-Adobe5k-UPE

消融实验

和其他方法对比

Attention-based network for low-light image enhancement

主要贡献

• 设计了一个端到端的应用于原始图像的增强网络，结合了 通道注意力 和 空间注意力模式，结合了局部和全局信息。
• 为了减少信息损失，设计了一个 ISL层 来 取代 max pooling
• 在SID数据集上评估了算法的有效性

Non-local operation

原始文献：Non-Local neural networks

​ 传统的卷积神经网络 其实只关注 局部图像的相关信息，而如果要获得全局信息，要通过很多层的卷积堆叠来扩大感受野，进而使网络形成全局信息的关注。全连接就是non-local的，而且是global的。但是全连接带来了大量的参数，给优化带来困难。基于此，作者根据 传统计算机视觉方法中的 非局部均值去噪滤波 的思想，设计了应用于CNN的 non-local操作。

• non-local operations通过计算任意两个位置之间的交互直接捕捉远程依赖，而不用局限于相邻点，其相当于构造了一个和特征图谱尺寸一样大的卷积核, 从而可以维持更多信息。
• non-local可以作为一个组件，和其它网络结构结合，用于其他视觉任务中

非局部均值去噪滤波

​ 传统的均值滤波的方法是 取目标像素位置的 领域区域的所有像素均值作为该位置滤波后的结果。而非局部的特点就是根据根据该局部区域和全局区域的相似度 作为加权系数来 加权平局。具体的过程如下图

w(x,y)一般定义为一个与欧式距离(2范数)相关的函数，设x，y的邻域宏块的欧式距离为d。对于待求位置x处的输出滤波，取x领域的小block 在周围大区域上滑动计算相似度，例如y位置处的相似度 d=||block(x)-block(y)||/block_size；则y加权到x点的加权因子为 w(x,y)=exp(-(dxd / (hxh))) 这个式子将原本的距离d转化为了 0-1之间的一个加权因子w(x,y)。h为衰减因子，h越小，加权因子越小，则加权点对当前点的影响越小，一般边缘保持得好但是噪声会严重，反之则边缘保持差图像更加光滑。计算欧式距离时，有时会考虑周围点对中心点的影响，会利用核函数对欧式距离加权。加权矩阵W要归一化。参考链接：https://blog.csdn.net/qianhen123/article/details/81043217

Non-local 表达式

\[\mathrm{y}_{i}=\frac{1}{\mathcal{C}(\mathrm{x})} \sum_{\forall j} f\left(\mathrm{x}_{i}, \mathrm{x}_{j}\right) g\left(\mathrm{x}_{j}\right)\]

​ 上面的公式中，输入是x，输出是y，i和j分别代表输入的某个空间位置，x_i是一个向量，维数跟x的channel数一样，f是一个计算任意两点相似关系的函数，g是一个映射函数，将一个点映射成一个向量，可以看成是计算一个点的特征。也就是说，为了计算输出层的一个点，需要将输入的每个点都考虑一遍，而且考虑的方式很像attention：输出的某个点在原图上的attention，而mask则是相似性给出。参看下图

为了简化问题，作者简单地设置g函数为一个1*1的卷积。相似性度量函数f的选择有多种。具体参考链接：

https://zhuanlan.zhihu.com/p/33345791 https://blog.csdn.net/shanglianlm/article/details/104371212

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#### pytorch  non-local实现
import torch
import torch.nn as nn
import torchvision


class NonLocalBlock(nn.Module):
    def __init__(self, channel):
        super(NonLocalBlock, self).__init__()
        self.inter_channel = channel // 2
        self.conv_phi = nn.Conv2d(in_channels=channel, out_channels=self.inter_channel, kernel_size=1, stride=1,padding=0, bias=False)
        self.conv_theta = nn.Conv2d(in_channels=channel, out_channels=self.inter_channel, kernel_size=1, stride=1, padding=0, bias=False)
        self.conv_g = nn.Conv2d(in_channels=channel, out_channels=self.inter_channel, kernel_size=1, stride=1, padding=0, bias=False)
        self.softmax = nn.Softmax(dim=1)
        self.conv_mask = nn.Conv2d(in_channels=self.inter_channel, out_channels=channel, kernel_size=1, stride=1, padding=0, bias=False)

    def forward(self, x):
        # [N, C, H , W]
        b, c, h, w = x.size()
        # [N, C/2, H * W]
        x_phi = self.conv_phi(x).view(b, c, -1)
        # [N, H * W, C/2]
        x_theta = self.conv_theta(x).view(b, c, -1).permute(0, 2, 1).contiguous()
        x_g = self.conv_g(x).view(b, c, -1).permute(0, 2, 1).contiguous()
        # [N, H * W, H * W]
        mul_theta_phi = torch.matmul(x_theta, x_phi)
        mul_theta_phi = self.softmax(mul_theta_phi)
        # [N, H * W, C/2]
        mul_theta_phi_g = torch.matmul(mul_theta_phi, x_g)
        # [N, C/2, H, W]
        mul_theta_phi_g = mul_theta_phi_g.permute(0,2,1).contiguous().view(b,self.inter_channel, h, w)
        # [N, C, H , W]
        mask = self.conv_mask(mul_theta_phi_g)
        out = mask + x
        return out


if __name__=='__main__':
    model = NonLocalBlock(channel=16)
    print(model)

    input = torch.randn(1, 16, 64, 64)
    out = model(input)
    print(out.shape)

主要方法

网络结构

Inverted Shuffle Layer

​ 作者说 设计这个的目的是因为常规的max pooling 虽然可以将低计算量但是会损失较多的信息，因此作者将 shuffle的思想应用到这个设计中。文章没有具体描绘结构 只是文字表述了一下，没懂到底怎样的结构

Inspired by pixel shuffle in [18], we proposed a new pooling operation, named ISL, which includes inverted shuffle and convolution operation. After an inverted shuffle operation, the size of the feature map reduces to half of the original and the number of channels quadruples. Convolution layer with 1×1 kernels is performed after the inverted shuffle, which plays a role in selecting useful information while compressing the number of channels. In general, ISL not only has the effect of reducing the computation as a pooling layer but also makes the network more flexible to select features.

损失函数

就是采用常用的 SSIM 和 L2损失结合。

实验结果

训练

这个文章可以算 learn to see in the dark 文章的补充，和它一样使用原始图像数据，只不过将注意机制等融入网络设计。训练集和测试集都是用的 SID。

结果

图像直方图

直方图均衡化

https://zhuanlan.zhihu.com/p/44918476

假如图像的灰度分布不均匀，其灰度分布集中在较窄的范围内，使图像的细节不够清晰，对比度较低。直方图均衡化，对图像进行非线性拉伸，是一种灰度的变换过程，将当前的灰度分布通过一个变换函数，变换为范围更宽、灰度分布更均匀的图像。这样，原来直方图中间的峰值部分对比度得到增强，而两侧的谷底部分对比度降低，输出图像的直方图是一个较为平坦的直方图。

原理

计算步骤

1. 计算原始图像的直方图
2. 计算累计直方图 CDF
3. 映射为 256 /（m x n ） x CDF

1
2
3
4
5
6
7
8
9
10

# calculate histogram
hists = histogram(img)

# caculate cdf
hists_cumsum = np.cumsum(hists)
const_a = level / (m * n)
hists_cdf = (const_a * hists_cumsum).astype("uint8")

# mapping
img_eq = hists_cdf[img]

直方图匹配

https://blog.csdn.net/qq_31347869/article/details/89514253

如果希望得到具有规定形状的直方图，就需要用到一种特殊的处理方法：直方图匹配 (直方图规定化)。原理很简单，有了参考图，可以计算它到规范化后的变换 ，同时也可以计算 低光图到 规范化后的变换。r -> s -> z s是中间规范化后的像素值 。最后求逆映射的时候不用显式的求，找最近的即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
img = cv2.imread('C:\\Users\\admin\\Desktop\\original_img3\\testimg\\lena_300_500.jpg')
ref = cv2.imread('C:\\Users\\admin\\Desktop\\original_img3\\testimg\\messi_300_500.jpg')
 
out = np.zeros_like(img)
_, _, colorChannel = img.shape
for i in range(colorChannel):
    print(i)
    hist_img, _ = np.histogram(img[:, :, i], 256)   # get the histogram
    hist_ref, _ = np.histogram(ref[:, :, i], 256)
    cdf_img = np.cumsum(hist_img)   # get the accumulative histogram
    cdf_ref = np.cumsum(hist_ref)
 
    for j in range(256):
        tmp = abs(cdf_img[j] - cdf_ref)
        tmp = tmp.tolist()
        idx = tmp.index(min(tmp))   # 找近似 即为逆映射
        out[:, :, i][img[:, :, i] == j] = idx
 
cv2.imwrite('C:\\Users\\admin\\Desktop\\lena.jpg', out)
print('Done')

局部对比度增强

就是将全局直方图均衡的思想应用于邻域直方图处理中

泊松方程

https://zhuanlan.zhihu.com/p/68349210

什么是泊松方程

所以需要知道图像周围一圈的边界值，那么上述的方程就有解了。这就是边界条件。边界条件一般有两种：

• Neumann 边界，译为纽曼边界或黎曼边界，给出函数在边界处的二阶导数值；
• Dirichlet 边界，狄利克雷边界，给出边界处函数在边界处的实际值。

但给定边界条件之后，就可以有 16 个方程式组成的方程组了，矩阵化表示此方程组之后，得到形式为 Ax = b

可以通过离散正弦变换加速泊松方程的求解，复杂度为N log(N)

泊松融合

泊松融合的思路就是 将源图像的目标图像的 梯度 图 使用 mask 拼接后，使用泊松方程把mask后的梯度图还原出融合后的图

A Fast Approximation of the Bilateral Filter using a Signal Processing Approach

双边滤波

​ 和高斯滤波一样都是用周围像素的加权平均的方式来代替某个像素点的亮度。与高斯滤波不同的是，双边滤波不仅考虑了中心像素和周围像素之间的欧式距离，还考虑了像素间的差异。使得双边滤波具有保持边缘的同时又具有平滑降噪的效果。如下图。高斯滤波器在图像的任意位置采用相同的高斯核, 这种处理的缺点是在实现对图像的有效平滑的同时也模糊了边缘信息, 图像的边缘区域不能很好的保持。

由定义可以看出, 在高斯滤波的基础上双边滤波器加入了正则系数和值域权重, 双边滤波里的两个权重域的概念：空间域（spatial domain S）和像素值域（range domain R）, 这个是它跟高斯滤波等方法的最大不同点。

• 在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊
• 在图像的平坦区域，像素值变化很小，对应的像素范围域权重接近于1，此时空间域权重起主要作用，相当于进行高斯模糊

快速双边滤波

​ 直接计算的话，上述运算量很大 因为每个位置的 值域的 权重都得重新计算。；滤波窗口越大计算量也越大。快速算法的思想是在原本的二维图像上增加一个新的值域维度。然后使用3维卷积滤波，加速计算。下面以一个一维信号来举例。

• 第一步创建双边网格。将整个网格初始化为0 。对于上右图所示的一维信号而言，如果不考虑downsample unsample sliceing的过程。将一维信号变为二维的方法就是 若原信号x位置的 值 为20，则对于 左边的wi 双边网格的 (x,y) 坐标 填充为20； 右边的w双边网格的 (x, y) 坐标位置填充 1 (为填充的位置初始为0) 这样将原始x信号依次填充 网格
• 使用一个二维高斯核 分别对 上述的wi ，w 双边网格滤波。高斯核的横轴代表空域，纵轴代表像素值域。可以 想想，原本x空域相邻的两个位置的值如果 差别很大，比如2和200，在填充双边网格时，他们在值域（图中的y轴）会被拉的很开，此时二者之间的关联在滤波核y方向的作用下被削弱甚至完全抑制。
• wi / w 做除法。之所以做除法是保证加权滤波的权重和为1。从图中可以看出在第二步滤波中，实际有很多为 0 的位置（其实就是没有像素对应的位置）也参与了滤波，因为这些为0的无效位置也占了权重，因此如果不归一化会拉低像素值。相当于 (0.5x20 + 0.3x15 + 0.2x0) / (0.5x1 + 0.3x1 + 0.2x0) 其中右边为0 的位置就是不存在像素的位置。而双边网格 i (0/1 标记有意义和无意义的位置) 的目的就是记录有效像素的滤波核的权重和。

​ 对于二维图像，增加一个值域坐标轴 就是三维的了 过程类似。同时为了降低计算量。原文作者的双边网格其实是在较原图较小的分辨率上做的。对于在一个bin里面的很多像素取平均.... 在低分辨率下得到的双边网格最后插值的方法上采样即可。具体算法流程如下：

面经 C++ 编译和底层