汇总了刷题中遇到的 图 相关的题目,例如拓扑排序,最短路径等
图
拓扑排序类
leecode:课程表 II
现在你总共有 n 门课 0 ~ n-1。想要学习课程 0,要先完成课程 1,用 [0,1] 表示。给定课程总量以及它们的先决条件,返回学完所有课程的顺序(返回一种即可),如果不可能完成所有课程,返回空数组。
这道题是一个典型的拓扑排序的问题,或者说 :
- 能拓扑排序 的图,一定是有向无环图
- 有向无环图,一定能拓扑排序
AOV网(Activity On Vertex Network):将一个工程分为多个小的活动(Activity),在有向无环图中,用顶点表示活动,用弧(有向边)表示活动的先后关系,简称为AOV网。
此题还可以使用 深度优先遍历,遍历所有节点,若节点未被访问则从该节点开始深度遍历。并将该节点状态设置为正在遍历中 1;当他的所有邻接子节点遍历完成后,再次回溯到这个节点时,将状态设置为 2 并将该节点入栈。 代表访问完成。而当该节点状态为 正在遍历中 并再次访问到它时 代表有环 直接退出,无拓扑排序。 最后输出时将 栈 反序输出即可。这么做可以成立的原因是,因为 节点入栈实在回溯的时候完成的 因此对于有出度的节点 它入栈的顺序一定晚于 由该节点输出的子节点,符合拓扑排序的要求。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
private:
vector<vector<int>> edges;
vector<int> indeg;
vector<int> result;
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indeg.resize(numCourses);
for (const auto& info: prerequisites) {
edges[info[1]].push_back(info[0]);
++indeg[info[0]];
}
queue<int> q;
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
int u = q.front();
q.pop();
result.push_back(u);
for (int v: edges[u]) {
--indeg[v];
if (indeg[v] == 0) {
q.push(v);
}
}
}
if (result.size() != numCourses) {
return {};
}
return result;
}
};
|
最短路径类
实例:LeeCode 743题
这个题从无向图的最短路径衍生而来。但是区别是这里有转机次数限制条件。因此如果没有跳转次数限制,存储起点到各节点的数组一维就够了,如果是有跳转次数限制,则最短距离数组为两维,新增的第二维为跳转次数:即从起点到节点 j 且跳转次数为 k 的最短距离。因为:如下情况 从A 出发到 节点 C 的最短路径是A->B->C 但是转了一次,如果从C 往后还有节点,但是只设置了一维最短距离数组,那么当取出{ C, 5, 0} 时由于 d[5] = 4 < 0 + 5 = 5(d[5] 被 A->B->C这个选项先更新为4了),就不会把 {C, 5, 0} (A->C) 路径加入优先队列,导致后面可能经过C到达节点N的最短路径且满足转机次数要求的路径 是A->C->… 这种情况被忽略。所以这个题加入了 转机次数的限制,最短路径就要为 两维数组,保存在转折次数相同时到达节点N的最短距离。
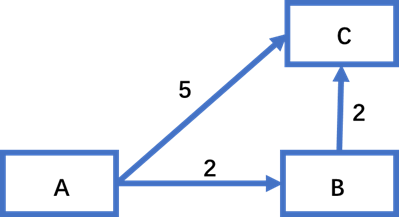 image-20210104223320648
image-20210104223320648
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
struct cmp{
bool operator() (vector<int>& a, vector<int>& b)
{
return a[1] > b[1];
}
};
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
vector<vector<int>> map(n, vector<int>(n, INT_MAX));
vector<int> d(n);
for(int i = 0; i < flights.size(); i ++){
map[flights[i][0]][flights[i][1]] = flights[i][2];
}
priority_queue<vector<int>, vector<vector<int>>, cmp> edges;
edges.push({src, 0, 0});
while(!edges.empty()){
vector<int> edge = edges.top();
edges.pop();
int p = edge[0];
int dis_tmp = edge[1];
int trans = edge[2];
if(p == dst) return dis_tmp;
for(int ed = 0; ed < n; ed++){
if(map[p][ed] == INT_MAX || d[ed] <= map[p][ed] + dis_tmp) continue;
d[ed] = min(d[ed], map[p][ed] + dis_tmp);
edges.push({ed, d[ed], trans+1});
}
}
return -1;
}
};
|
并查集
主要用途是 (参考链接:https://blog.csdn.net/liujian20150808/article/details/50848646)
求联通分量:依次对每个边的两个顶点进行并查集合并,可以使得每个连通分量的root相同,从而得出每个连通分量。
查找环: 合并过程中,如果发现一条边的两个顶点已经合并过,说明这两个顶点之前已经通过其他路径合并,再加上这条边,图中就出现了环。合并节点 a , b 时 发现它两是一个祖先,是无向图,这样再加上边a-b就构成了环。(leecode 684 冗余连接)
求最小生成树: 贪心思想,从小到大排序所有边,使用并查集依次合并,并跳过形成环的边,即可得到最小生成树。
基本用方法 (详情 ):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public:
vector<int> parent;
int set_cnt;
int find(int i){
int p = i;
while(parent[p] != p)
p = parent[p];
parent[i] = p;
return p;
}
bool unio(int p, int q){
int rootP = find(p);
int rootQ = find(q);
if(rootP == rootQ)
return false;
parent[rootP] = rootQ;
set_cnt--;
return true;
}
void init(int N){
set_cnt = N;
parent.resize(N);
for(int i = 0; i < N; i++){
parent[i] = i;
}
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
init(edges.size()+1);
for(vector<int> edg : edges){
if(unio(edg[0], edg[1]) == false)
return edg;
}
return {};
}
};
|
最小生成树
是 一副连通加权无向图中一颗权值最小的生成树。
Kruskal 克鲁斯卡算法
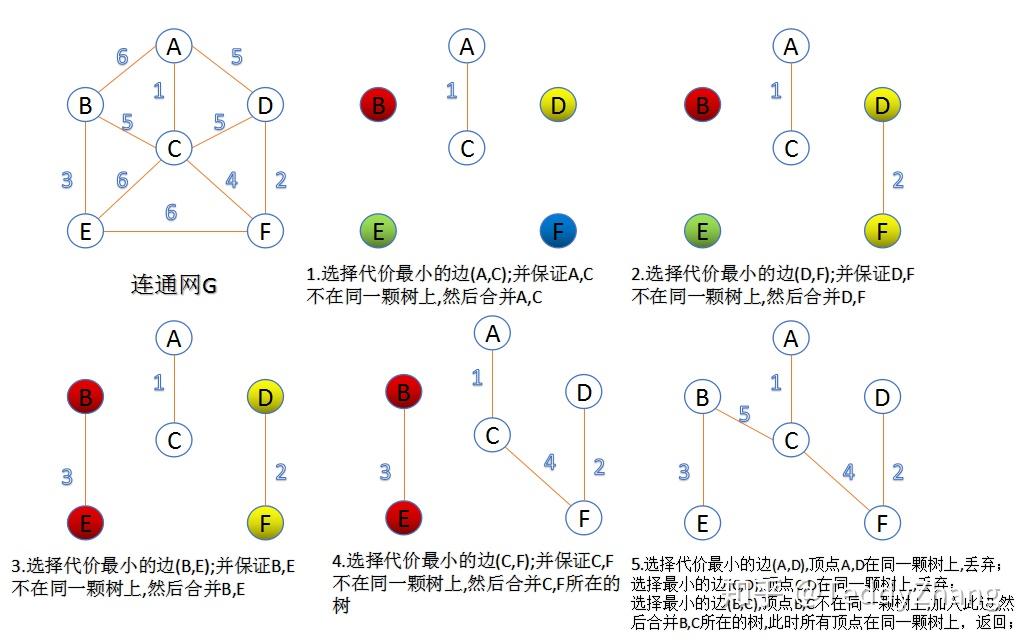
Kruskal 算法是一种贪心算法,将图中的每个edge按照权重大小进行排序,每次从边集中取出权重最小且两个顶点都不在同一个集合的边加入生成树中!注意:如果这两个顶点都在同一集合内,说明已经通过其他边相连,因此如果将这个边添加到生成树中,那么就会形成环!这样反复做,直到所有的节点都连接成功!这里可以用前面的并查集实现,复杂度NlogN
leecode: 找到最小生成树里的关键边和伪关键边
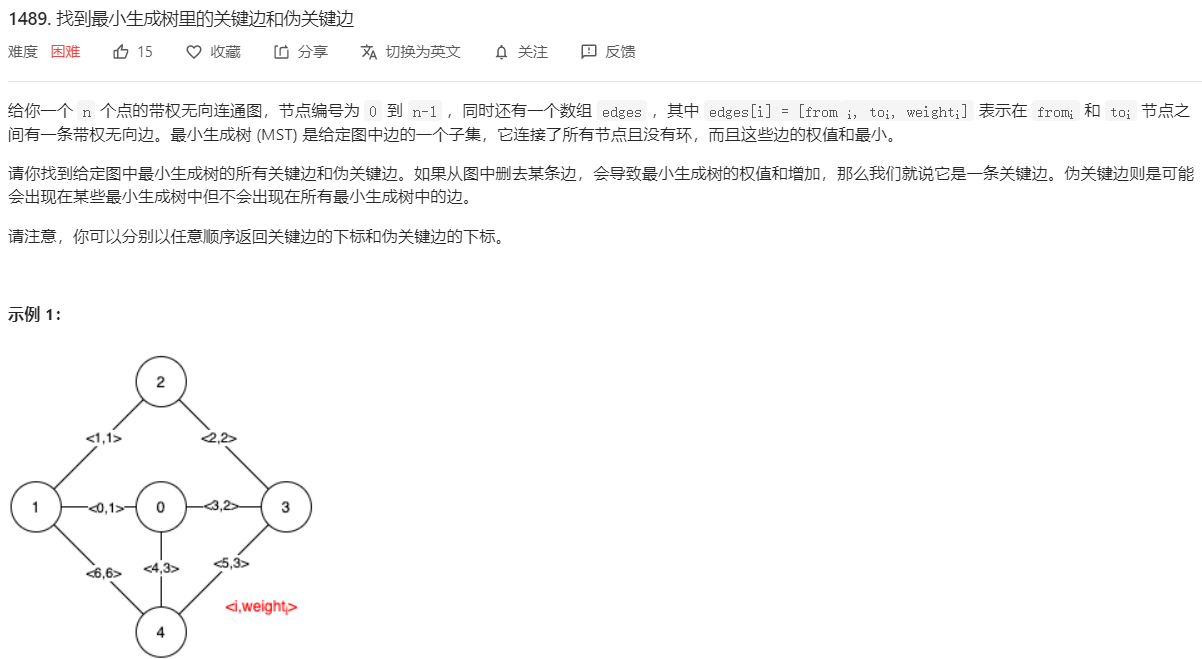
较简单的暴力思想。首先使用 kruskal算法+并查集的方法 求得最小生成树的 最小权值。然后再遍历判断每个边是否为 关键边。例如对于边 i 。判断它是关键边的方法就是在 使用 kruskal 时 跳过该边。如果最后生成的树的权值比开始计算的大 或者 不连通,说明它是关键边。伪关键边只会出现在 权值相同的多个边中,因此在生成树的时候优先以 待判断的边去选择,再对比最后生成树的权值是否最小。


