详细记录了 KMP 算法的原理,KPM算法是一种字符串匹配算法,可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。
KMP 算法
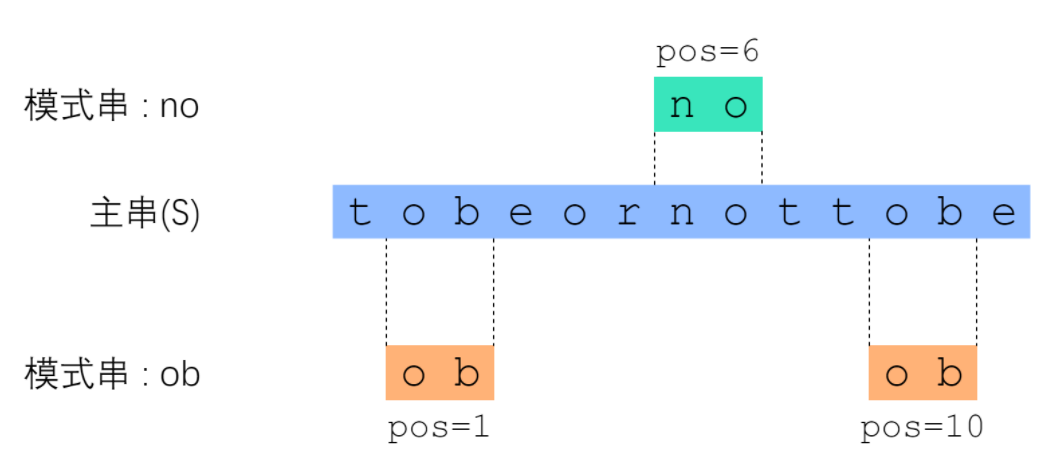
KMP算法是一种字符串匹配算法,可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。如下图所示,字符串匹配就是从主串中搜索是否存在模式串。字符串匹配是一个非常频繁的任务。例如,今有一份名单,你急切地想知道自己在不在名单上;又如,假设你拿到了一份文献,你希望快速地找到某个关键字(keyword)所在的章节……凡此种种,不胜枚举。
暴力 Brute-Force
首先想到的就是 暴力搜索,从最开始对齐比较 如果不相同,将模式串往后移动一位再去和主串对应位置的子串比较….直到找到。但是显然这样比较的复杂度为O(n*(m-n+1)) n 为主串的长度,m为子串的长度。
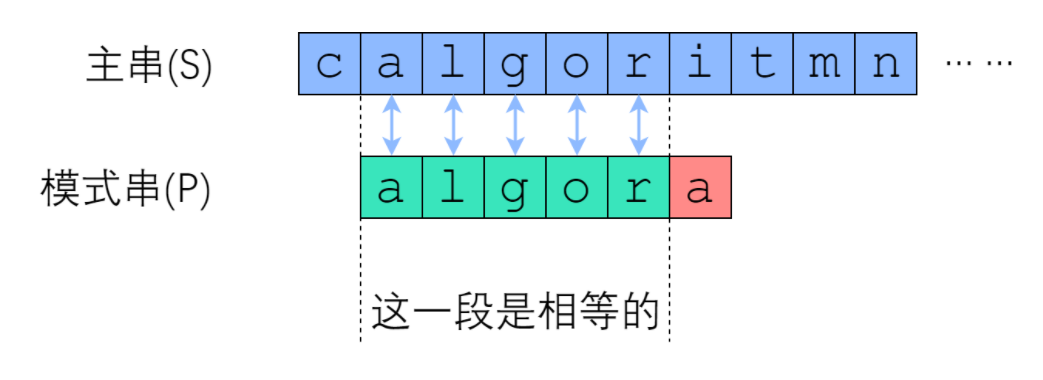
暴力的方法很慢,那么有没有优化的方法了。暴力方法中每次 没匹配上 都是往后移动一格,然后接着比较,这样比较的趟数很多,完全没有用到上一次比较失败的教训。尽可能利用残余的信息,是KMP算法的思想所在。上面的例子中在匹配 algor 全对上了,但是最后一个a没有匹配上,按照暴力的逻辑 可能就往后滑动一个 再接着配。但是我们可以明显看出 algor 这几个字母如果错位,就不可能再配上,所以完全可以从 i 去比较,可以直接跳过主串中algor这几个字母。再例如下面的例子:
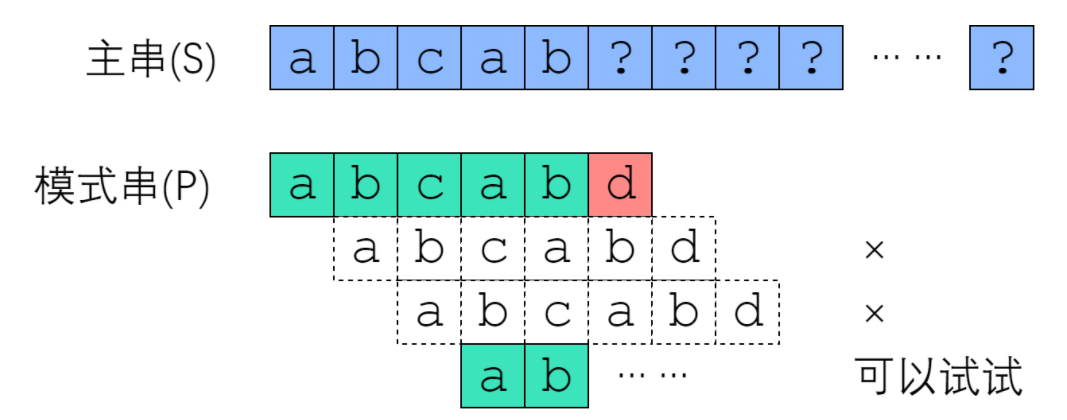
还是在 最后一个 d 处对不上,但是已经比较了 abcab 这一段,这一段模式串和主串是对的上的,根据这个已知信息 按照直觉逻辑,这次可以跳到ab试试,因为可以保证 模式串中已经比较过的 ab 和 主串中的部分对的上,而且 比较过的这一段中 存在首ab 和 尾ab相同。一句话总结 我们在已经比较并确定对齐的模式串的主串abcab后,我们移动的准则是 从abcab中 找到 模式串的首ab 和主串的尾ab对齐的位置,再往后就是主串之前没比过的位置就接着比 。这是KMP算法的核心了。
KMP原理
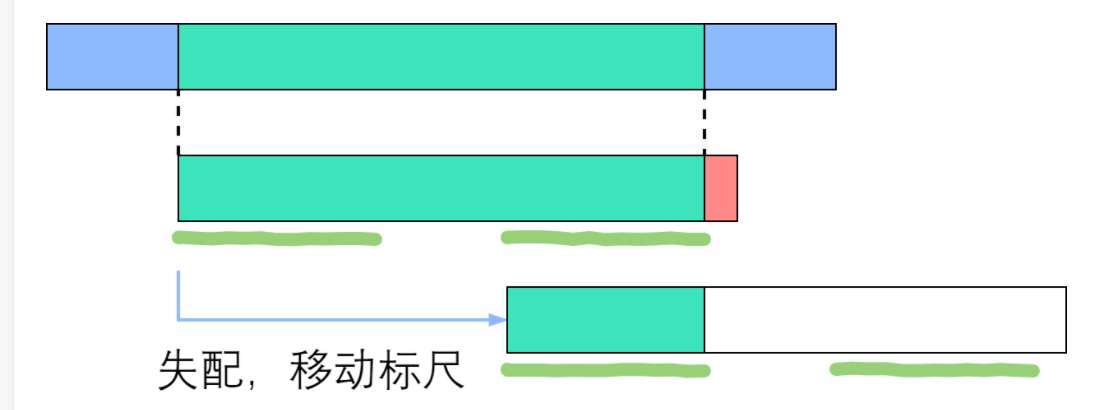
如上图所示,绿色部分是成功匹配,失配于红色部分。深绿色手绘线条标出了相等的前缀和后缀,其长度为next[右端]. 由于手绘线条部分的字符是一样的,所以直接把前面那条移到后面那条的位置。因此说,next数组为我们如何移动标尺提供了依据。
PMT表
上述 ab … ab 这样首位相同的结构,叫做前缀和后缀。(也叫 next 数组 即 PMT表)
如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。要注意的是,字符串本身并不是自己的后缀。
如果一个字符串长度为N 那么PMT表的长度就为N 定义为:PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如 对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。
构建next数组
next数组是 针对模式串的。next数组的定义:
- 定义 “k-前缀” 为一个字符串的前 k 个字符; “k-后缀” 为一个字符串的后 k 个字符。k 必须小于字符串长度。
- next[x] 定义为: P[0]~P[x] 这一段字符串,使得k-前缀恰等于k-后缀的最大的k.
用动态规划的思路思考,如果已知 next[0] next[1] next[2] … next[x] 要求 next[x+1]呢?首先,已经知道了 next[x-1](以下记为now)。
- 如果 P[x] 与 P[now] 一样 (图中的是不相等的情况) 最长相等前后缀的长度就可以扩展一位,很明显 next[x] = now + 1。
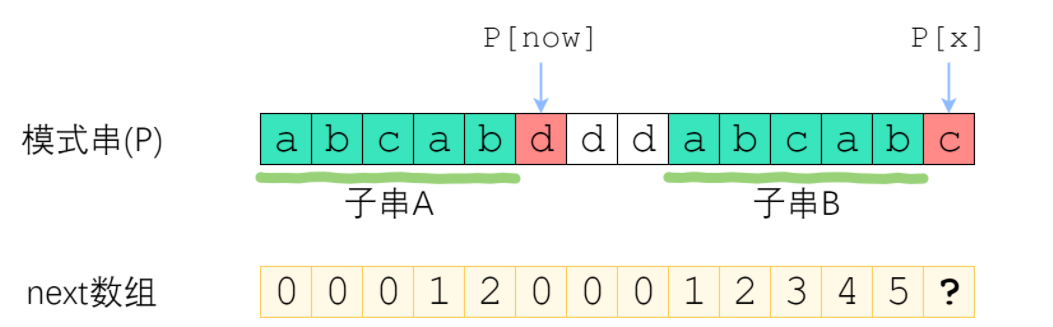
- P[x] 与 P[now] 不一样 。如上图 不能直接+1,因此,我们应该缩短这个now。 但是还是可以知道字串A == 字串B(这是由next[x]确定已知的),后面要新增一个 c 所以这个 c 肯定要用上,那么我们希望从 字串 B 的尾巴(后缀集合)中找一段 假设为 C , 和字串A 的前缀中找一段 假设为 E 满足 C + ‘c’ == E,把 E 拆开为 E1 + 字符n ,又字串A == 字串B,这不就等于在子串 A 中 找相等的最大前缀C和后缀E (回到了next的定义 即为next[now - 1] ),然后再判断‘c’ 是否等于字符n。综上:
- now = next[ now - 1]
- 再判断 p[x] == p[now] 是否成立,成立就是 next[now - 1] + 1 否则循环
代码

