汇总了编程中常用的编程思想的原理，例如DFS，动态规划，回朔等

算法思想汇总

广度/深度优先搜索 BFS/DFS

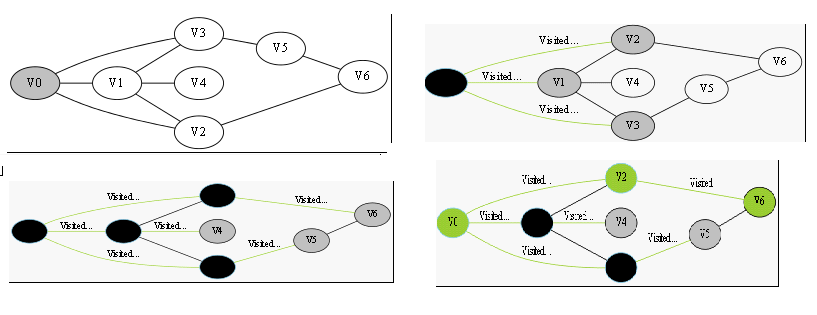
​ 广度优先搜索 是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域 BFS同样属于盲目搜索。一般用队列数据结构来辅助实现BFS算法。

1. 首先将根节点放入队列中。
2. 从队列中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
3. 若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
4. 重复步骤2。

1598357141189

/**
 * 广度优先搜索
 * @param Vs 起点
 * @param Vd 终点
 */
bool BFS(Node& Vs, Node& Vd){
	queue<Node> Q;
	Node Vn, Vw;
	int i;
 
	//初始状态将起点放进队列Q
	Q.push(Vs);
	hash(Vw) = true;//设置节点已经访问过了！
 
	while (!Q.empty()){//队列不为空，继续搜索！
		//取出队列的头Vn
		Vn = Q.front();
 
		//从队列中移除
		Q.pop();
 
		while(Vw = Vn通过某规则能够到达的节点){
			if (Vw == Vd){//找到终点了！
				//把路径记录，这里没给出解法
				return true;//返回
			}
 
			if (isValid(Vw) && !visit[Vw]){
				//Vw是一个合法的节点并且为白色节点
				Q.push(Vw);//加入队列Q
				hash(Vw) = true;//设置节点颜色
			}
		}
	}
	return false;//无解
}

​

回溯

简介

Backtracking（回溯）属于 DFS

• 回溯算法就是按照深度优先的顺序，穷举所有可能性的算法，但是回溯算法比暴力穷举法更高明的地方就是回溯算法可以随时判断当前状态是否符合问题的条件。一旦不符合条件，那么就退回到上一个状态，省去了继续往下探索的时间
• 优化剪枝策略，就是判断当前的分支树是否符合问题的条件，如果当前分支树不符合条件，那么就不再遍历这个分支里的所有路径。
• 启发式搜索策略指的是，给回溯法搜索子节点的顺序设定一个优先级，从该子节点往下遍历更有可能找到问题的解。
• 普通 DFS 主要用在 可达性问题 ，这种问题只需要执行到特点的位置然后返回即可。
• 而 Backtracking 主要用于求解 排列组合 问题，例如有 { 'a','b','c' } 三个字符，求解所有由这三个字符排列得到的字符串，这种问题在执行到特定的位置返回之后还会继续执行求解过程。

​ 该页中 平洋大西洋水流问题 中解释中的，将他看作从四周到中间可达问题比较简单，但是自己第一次做的时候其实是用的回溯的思想做的，比较复杂。 因为 Backtracking 不是立即返回，而要继续求解，因此在程序实现时，需要注意对元素的标记问题：

步骤

​ 回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。用回溯算法解决问题的一般步骤：

1. 在访问一个新元素进入新的递归调用时，需要将新元素标记为已经访问，这样才能在继续递归调用时不用重复访问该元素；

2. 但是在递归返回时，需要将元素标记为未访问，因为只需要保证在一个递归链中不同时访问一个元素，可以访问已经访问过但是不在当前递归链中的元素。

贪心算法

​ 贪心算法，又名贪婪法，是寻找最优解问题的常用方法，这种方法模式一般将求解过程分成若干个步骤，但每个步骤都应用贪心原则，选取当前状态下最好/最优的选择（局部最有利的选择），并以此希望最后堆叠出的结果也是最好/最优的解。

1. 从某个初始解出发；
2. 采用迭代的过程，当可以向目标前进一步时，就根据局部最优策略，得到一部分解，缩小问题规模；
3. 将所有解综合起来。

双指针

​ 双指针 有 快慢指针 和 左右指针 。双指针法充分使用了数组有序这一特征，从而在某些情况下能够简化一些运算。前者解决主要解决链表中的问题，比如典型的判定链表中是否包含环；后者主要解决数组（或者字符串）中的问题，比如二分查找。

快慢指针 ： 般都初始化指向链表的头结点 head ，前进时快指针 fast 在前，慢指针 slow 在后。

• 判定链表中是否含有环。从head出发， 快指针每次移动慢指针两倍的距离，二者相遇则有环，快指针先结束无环。
• 返回环的长度。相遇后，固定一个指针不懂，移动另一个到再次相遇 记录走过的步长 即为环的长度
• 返回环的起点。在刚才相遇的B点，将一个指针回归到起点，另一个还是在B点，然后二者以相同的速度移动，二者再次相遇的 点即为换的起点。具体证明可画图 理解。
• 返回链表的中点。类似上面的思路，让快指针一次前进两步，慢指针一次前进一步，当快指针到达链表尽头时，慢指针就处于链表的中间位置。
• 寻找链表的倒数第 k 个元素。让快指针先走 k 步，然后快慢指针开始同速前进。当快指针走到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点。

左右指针： 左右指针在数组中实际是指两个索引值，一般初始化为 left = 0, right = nums.length - 1。当数组提到有序时就应该想到双指针。

• 二分查找，反转数组，两数之和…
• 滑动窗口算法 。滑窗的关键在于判断什么时候座指针收缩窗口，何时更新数据，合理的收缩窗口的方法可以大大简化代码。

二分查找

​ 二分查找也称为折半查找，每次都能将查找区间减半，这种折半特性的算法时间复杂度为 O(logN)。

​ m 计算： m = l + (h - l) / 2 ​ 未成功查找的返回值：循环退出时如果仍然没有查找到 key，那么表示查找失败。可以有两种返回值。-1：以一个错误码表示没有查找到 key；l：将 key 插入到 nums 中的正确位置。 ​ 变种：二分查找可以有很多变种，实现变种要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下：

public int binarySearch(int[] nums, int key) {
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int m = l + (h - l) / 2;
        if (nums[m] >= key) {
            h = m;
        } else {
            l = m + 1;
        }
    }
    return l;
}

分治算法

​ 分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

​ 适用的情况：

1. 该问题的规模缩小到一定的程度就可以容易地解决
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

​ 分治法在每一层递归上都有三个步骤：

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
2. 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3. 合并：将各个子问题的解合并为原问题的解

常见的例如 二分搜索，汉诺塔问题，归并排序，快速排序等都是使用分治的思想。