0%

相关的编程题汇总-表

发表于 更新于 分类于 ，

汇总了刷题中遇到的 表 相关的题目，例如栈，哈希表，数组字符串相关的题目

数组/字符串

旋转图像

要做到不占用额外空间

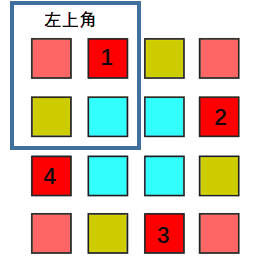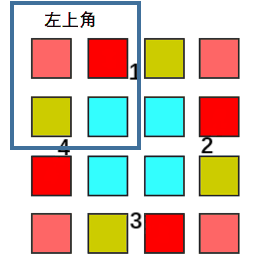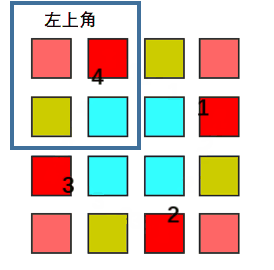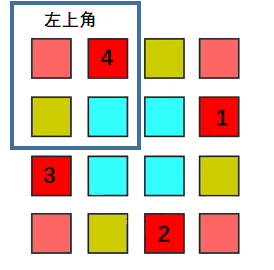
rotate.gif

方法一：需要用 暂存一个值 然后 循环交换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for (int i = 0; i < n / 2; ++i) {
            for (int j = 0; j < (n + 1) / 2; ++j) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;
            }
        }
    }
};

方法二：先水平镜像 后竖直镜像

计算器

方法一：递归的方法 很好理解。用递归 实际上也是 遍历了一边确定没有乘除之后 再遍历一圈计算加减

定义函数计算 cal(string &s, int l, int r) 字符串s在区间[l,r]的结果

  1. 由于是递归所以优先级低的+-先判断进入递归
  2. 因为同等优先级是从左往右 所以递归是从右往左开始扫
  3. 如果没有符号则说明这个区间里是一个数字 使用 stoi 返回数字即可

方法二：使用堆栈 只遍历一次。遇到乘除直接计算值，遇到加减，将数字放入堆栈（带符号的放入），最后计算堆栈中所有数字的和

验证IP地址

这个题 很恶性 主要就是各种边界条件的判定。有三种方法：

  1. 不使用任何库函数 就纯c++手写循环。使用状态机的思路 构建了状态表 逻辑比较清晰 不会乱
  2. 使用 stringstream 来分割字符串
  3. 使用 正则表达式 这种方法最慢，但是代码最简介。

移除无效的括号

寻找两个正序数组的中位数

这个题要求实现 log(m+n)的时间复杂度。首先想到的是使用 归并的方式从头到尾寻找中位数。但是这样复杂度是O(m+n)。不符合要求。看到log(m+n)首要想打就是 二分法。问题是这个怎么用二分法呢。

首先找中位数 就是找第k个数，那么我就上下 各找前 (k-1)/2个数，然后比较两个数组这个位置数字大小，因为数组是有序的，一旦比较大小比出结果，就可以排除一大部分数字。再在后面的区间中找.

重复的子字符串

一开始想到的是 暴力枚举 子字符串的个数，从2，3，4…. 字符串长度如果不能整除可以跳过。然后怎么判断 字符串是否是3个子串重复的呢？例如 a = a1 + a2 + a3 如果要判断a是三个重复的组成就要判断 a1 == a2 a2 == a3 都成立，这样写麻烦，直接把 比较（a2 + a3 + a1 ）== (a1 + a2 + a3) 是否相等即可，代码写着比较简便。

但是更好的方法是 双倍长度法 构建新的双倍长度的字符串 s == a + a 然后 从 s 的第1个元素开始查找 和 a 匹配的位置，如果a 没有重复字符串组成 那么 找到的位置一定是从 a.size() 开始，即只能找到后面那个 a。

下一个排列

这个题主要要想清楚下一个大排列的规律。 参考连接：https://leetcode-cn.com/problems/next-permutation/solution/xia-yi-ge-pai-lie-suan-fa-xiang-jie-si-lu-tui-dao-/

旋转数组

这个题很经典。要求不使用 额外的 空间将 数组平移。方法1是使用三次翻折法，比较好想。方法二是循环移位法，原理假如下：

假设现在有 A 、B 、C、 D、 E 五名同学，今天考试完，老师要求换座位，每个同学向后移动3个座位。于是就从 A 同学开始换座位了... A同学 非常自觉，看了看自己座位号（0），根据老师要求，他走到了3 号位置，即 D 同学的位置，同时他把D 同学赶到了角落，自己坐在了 3 号位置，第一个完成任务真爽！D同学 一看，不行啊，我咋能呆在角落，于是D同学也按要求理直气壮来到了1号位置，同样把B同学赶到了角落，猛男落泪...B同学 当然也不干，气汹汹走到了4号位置，"E同学，麻烦起来一下，角落给你收拾好了：)",于是 E同学来到角落..E同学 一想：不行呀，我这么帅，必须有座位！站起来跑到了2号位置，二话不说，赶走了C….

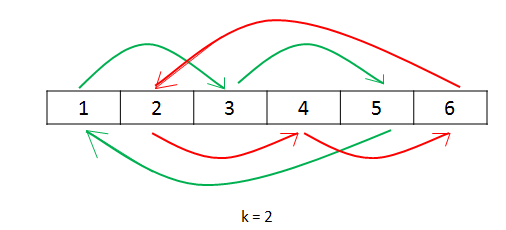
image-20210426110441307

同样，对于循环移位类的问题，可以这样理解，移动后的位置 i = (k + i) % len；但是移动的时候，可能还没遍历完所有的元素，就回到了起点。也可能从起点0开始，往后寻找，到下一轮回到了1位置，这时候再循环，可以到2位置….最终肯定能够再回到起点位置。也可能是从起点开始，到下一轮刚好又回到起点。

image-20210426113941474

链表

相交链表

双指针，走 m + n + c n + m + c 相遇

LRU 缓存机制

LFU 缓存

这个题和上面的区别在于，LRU的题意是，删除最久没使用过的元素，所以通过一个链表即可完成。而这个题要求删除使用最少的元素，所以就需要记录每个元素的使用次数。但是这个最小使用次数有一个规律，使用一个 变量 记录最小使用的次数，每次插入元素

  • 若该元素A在缓存中存在，且A的使用次数大于最少使用次数，那么该次插入对最小使用次数不影响
  • 若该元素A在缓存中存在，且A不是唯一一个使用次数最少的元素，那么将它的使用次数加1之后，还是不影响系统的最下使用次数
  • 若该元素A在缓存中存在，且正好A就是唯一的一个最少使用次数的元素，那么系统的最少使用次数 + 1 并将改元素移动到 使用频率为 min+1 的缓存池中
  • 若该元素A是个新元素，那么删除缓存中的最少使用频率的元素后，系统使用次数最少频率 就 是 1

综上，在这个操作逻辑下 想要维护系统最小使用次数这个变量，其实逻辑不复杂，不需要排序。因此优化上述的数据结构，可以很容易O(1) 实现所有功能

但是，如果想不到 上述 O(1) 的方法，想到要取出 频率最小的元素，其实就应该 想到 堆 二叉搜索树 等数据结构，但是 用堆，当插入的元素不是堆顶的元素的是偶，从堆中搜索其他元素，O(n) 所以，考虑使用 红黑树，来维护 使用频率的有效性。c++中 set 底层是 红黑树，自定义数据结构后对 < 重载，就可以保证插入到集合中的元素是有序的，每次取出集合起始的元素即可。（但是 要注意，自定义数据结构中，仅仅以 频率作为排序依据实不行的，因为不同元素使用频率可能一样，而集合要求每个元素不同，另外题目也要求 使用频率一样的 删除最近没使用的变量，所以新增一个 time（时间戳） 变量来标记每个元素，当有新的操作增加时，对应被操作的元素time更新时间戳，当使用频率相同时使用time的大小做为排序依据）。这种使用红黑树的方法，每次插入元素复杂度为 O(log N)

全 O(1) 的数据结构

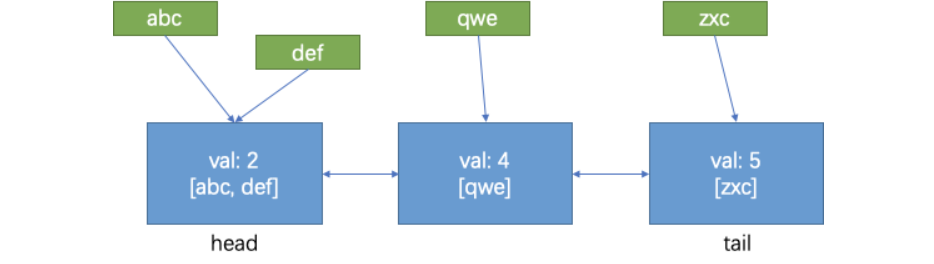
和 LFU 类似。这种 O(1) 一般都是要用Hash表，自己想的是以频率作为键来存储每个频率中的元素，但是当极端情况下 频率出现较大断层的 情况 {1: [“dsd“]， 55：[“sdsd”]} 这种情况，吧“dsd”删除后 寻找最小频率的复杂度就很高了，要向上搜索到55 所以更好的方法是 使用双向链表来 记录顺序，因为每次频率 只能是 +1 -1的操作，所以频率节点每次只会像周围移动一次，但是为了避免寻找特定 key 的节点，需要用 Hash表存储 key->Node的映射。

image-20210614154217494

回文链表

基本的方法是 遍历链表 把 每个节点缓存到数组里 然后使用双指针判断是不是 回文链表。空间复杂度O(1) 的方法是 先使用快慢指针找到链表的中点，然后将链表后半部分反转，再和前半部分比较，这样没有缓存任何东西，空间复杂度O(1) 时间复杂度O(N)

排序链表

很容易想到归并排序，但是在实现过程中 很容易出现 无线递归的情况。这样考虑 一个节点的时候 中点节点回是哪个，两个节点的时候中点节点会是哪个，基本四个以上的节点就不会出问题了 主要是节点少的时候容易无限递归。

合并K个升序链表

首先合并两个，然后再和第三个合并，再和第四个合并…. 这样时间复杂度为 O(KxKxN) 可以使用归并优化 降低时间复杂度

Hash表

O(1) 时间插入、删除和获取随机元素

vector 的尾部插入删除时间复杂度为O(1) 但是随机插入和删除的时间复杂度为O(N) 所以要解决随机删除复杂度的问题 可以记录 将要删除的某个元素在vector 中的位置然后将他和最后一个元素交换，然后把最后一个元素删了即可

缺失的第一个正数

这个题 有点意思 要时间复杂度 O(N) 常数的空间复杂度。首先一个隐含条件需要看出来，那就是缺失的最小正整数一定是[1, N+1]其中N为数组长度。所以要实现时间复杂度O(N)很容易，直接枚举N个数。用hash表判断每个枚举的数在不在表中即可。

但是要空间复杂度为O(N) 那就不能额外新建hash表了。但是题目给定的数组可以修改啊，于是乎 怎样在修改数组中数的前提下，害不修改数组的值呢？那就是用正负号标记喽。只对原数组中的数做 正负 处理，如果某个元素存在就将该元素对应的下标上的数 用负标记。（由于数组中可能会存在 0或这负数，而这些数肯定不是 要找的最小正整数，所以将他们预先设置为N+1，不影响负号的标记即刻）。最后再遍历，最先出现正数的位置（即每被标记过） 即为 最小的正数。

综上 遍历三次 第一次 将负数和0设置为 N+1，第二次遍历标记出现过的数对应的下标的值标为 负数，第三次遍历找第一次为正数的下标

最长连续序列

这个题不难实现，但是关键是先能想到的使用暴力的方法 求解的逻辑，然后再使用 Hash 去优化，最后再进行剪枝，最终实现 O(n)。

和为K的子数组

这个题还可以变化一下 和 大于 K 的最短子数组 就是另一个题目了

连续数组

这类 连续数组 和 >> 前缀后 >> 数组中两数差/两数和 >> Hash

单调栈

下一个更大元素 II

这是一个典型的单调栈的题目 。 就是栈中元素,按递增顺序或者递减顺序排列。

接雨水

单调递减栈。这个题，关键点 是没想到 怎么计算雨水的容量，一开始想的是 宽度x短边长，但是如果这里面还有其他矮的柱子，还得减去矮柱子的面积，想到了使用栈的方式，但是没想到使用栈的第推计算面积的方式，计算面积可以通过高度差的方式 累计面积。

其实这个题最好想的思路 不是用单调栈。按照题目意思，对于当前位置能存水的量是 min(左边最大高度, 右边最大高度) 那么问题就转换为 求每个位置左边最大高度，和右边最大高度。这就和 下面这个题有点类似，下面这个题最终就是要找每个位置 左边第一个右边第一个小于当前高度的柱子。但是后者用单调栈分别左右遍历可以求得，而前者使用最大值遍历即可求得。都需要两个方向遍历。

柱状图中最大的矩形

不同字符的最小子序列

相对简单的单调栈有更多限制，但是基本思想还是一样的。

和至少为 K 的最短子数组

分割数组

构建单调数组，基本的方法是两趟遍历分别寻找数组左边和右边的最大值，最小值。我一开始想的，因为从最左边到最右边滑动，相当于一个数据流，左边的数据不断增多，右边的数据逐渐减少，相当于两个数据流，通过堆的方式获取左边和右边的最大最小值。但是明显，在数组数据固定的时候可以通过O(N) 的方式求到每个位置得最大最小值，而用堆，复杂度至少O(NlogN)

栈

字符串解码

难度困难1400

队列

滑动窗口最大值

这个题 和 最大栈/单调栈 类似。只不过那个是用来记录栈数据中的最大值，因此需要一个额外的最大栈。这种题目中 最大值都是和元素的增加顺序有关，因为滑动窗口很像 双端队列的逻辑，所以使用一个双端队列来记录最大值。具体的 窗口前端增加数据时，首先队列前端所有比他小的元素，然后再将改元素从前端入队，同时窗口可能还要收缩一个单位，如果待收缩的元素不是队列尾端的，就不管，若是就从尾端弹出。最后窗口最大的元素就是队列末尾的元素了。o(N)

但是这个题也可以用优先队列做。首先优先队列中存放K个数，顶端的肯定是最大的，但是不一定在窗口中，因此每次去顶端元素时，要先保证它在窗口中（同时记录每个元素的大小 和 其在数组中的索引位置）即索引位置在窗口以外，就弹出，直到顶端元素在窗口中，那么顶端元素就是窗口的最大值。这个方法复杂度 O(log(N))