数据结构-图

数据结构之图，记录了图有关的定义和常规操作

图

几个重要的概念

• 有向图 / 无向图 / 混合图：每个边都是有向边，个边都是无向边，…
• 度：顶点相邻边的数目，常用 deg(V), d(v) 表示。有向图中 以该顶点为终点的边的数目 入度； 以该顶点为起点的边的数目 出度 ； 顶点的度 = 入度 + 出度。
• 连通的 / 连通图 / 连通分量 / 极大连通子图：从顶点 u 有路径到达 v ，则 u,v 是连通的；任意两点连通；H是G的连通子图，且不存在连通图F，使得 H ⊊ F ⊆ G，则H是G的连通分量。
  • 连通图只有一个连通分量，即图自身
  • 非连通图有多个连通分量。

图的表示

直接存边：使用一个数组来存边，数组中的每个元素都包含一条边的起点、终点和边权（带边权的图），或者使用多个数组分别存起点、终点和边权。

1598969422109

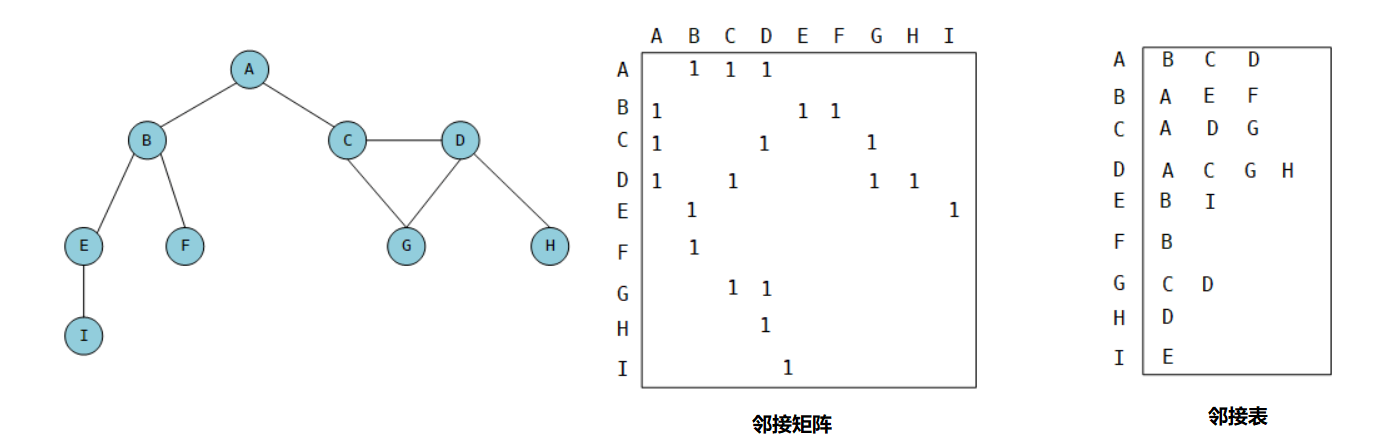
邻接矩阵 Adjacency Matrix二维数组 adj[][]，adj[u][v] 为 1 表示存在 u 到 v 的边，为 0 表示不存在。如果是带边权的图，可以在 adj[u][v] 中存储 u 到 v 的边的边权。

邻接表 Adjacency Table：使用一个支持动态增加元素的数据结构构成的数组，例如c++中的 vector

• 领接表：中 adj[u] 存储的是点 u 所有出边的信息（终点、边权等）

• 逆邻接表：中 adj[u] 存储的是点 u 所有入边的信息（起点、边权等）

  ​

图的遍历

• 深度优先搜索 (Depth-First Search, DFS)
• 广度优先搜索 (Breadth-First Search, BFS)

拓扑排序

根据依赖关系输入 排序结果，要将被依赖的步骤放在前面执行，没有依赖关系的步骤先后顺序无所谓。对于有环的图，构成了循环依赖的关系，因此这个环上的所有元素无法输出。所以 拓扑排序可以用来判断图是否有环

思路

广度优先

首先入度为0的节点，它一定不依赖任何节点，所以它可以最先输出。因此首先遍历所有节点并统计每个节点的 入度；一开始将所有入度为0的节点之间放入队列。按照广度优先遍历的套路，不断从队列中取节点，取出的节点代表它执行完毕，可以被输出，同时将它指向的节点的入度减1，如果减到了0那么就代表它所有的依赖都执行了，因此可以放入队列中等待执行（输出）。

深度优先

遍历所有节点，若节点未被访问则从该节点开始深度遍历。并将该节点状态设置为正在遍历中 1；当他的所有邻接子节点遍历完成后，再次回溯到这个节点时，将状态设置为 2 并将该节点入栈。 代表访问完成。而当该节点状态为 正在遍历中 并再次访问到它时 代表有环 直接退出，无拓扑排序。最后输出时将 栈 反序输出即可。这么做可以成立的原因是，因为 节点入栈实在回溯的时候完成的 因此对于有出度的节点 它入栈的顺序一定晚于 由该节点输出的子节点，符合拓扑排序的要求。

最短路径

深度/广度优先遍历

这种方法耗时较长。初始 到其他节点的延时为无穷大。首先从初始节点出发，开始广度/深度优先遍历。判断是否将新的节点加入队列的方法是 当前延时小，则将该节点加入访问队列（递归节点）。这样可以防止有环的情况下 出现死循环。对于广度优先遍历的方法，注意不能用 入度数 是否递减到 0 来判断 是否停止 将其加入遍历，例如 4->1->2->3 4->2->3 若第一个路劲 为最短 ，但是 若用入度数递减为0判断是否加入遍历的条件，路径一会先到达3这样导致 2->3提前失效，就无法找到最短的路径一。

迪杰斯特拉算法 Dijkstra

特点： （参考链接: https://blog.csdn.net/qq_35644234/article/details/60870719）

• 求单源最短路径，即求从一个点出发 到其他所有点的最短距离
• 只适用于非负权图
• 时间复杂度优秀
• 使用了贪心思想

步骤：

1. 初始化两个集合，一个已确定最短路径的节点为集合P， 未确定最短路的节点为集合Q。保存源节点 K 到每个节点的距离，若源节点和它无直接连接，初始化时距离为无穷大。将源节点K放入 P。
2. 从Q中找一个 到 K 距离最短的节点 u, 因为距离权值都是正，而这个又最短，其他的无论怎么从 K 走到 u 都不如这个 K直接到 u 的近。因此将它放入P，代表已经确定。 （贪心思想）
3. 上一步已经确定一个新的 最短路径的节点，这一步就要 确定 以 u 为出的 边所指向的 节点 v，是否能通过 u 缩短 K到v的距离。这一步叫松弛。此时 v 节点还是在Q中。
4. 循环 2 开始 找新的 最短距离 节点 然后再用新的最短边 来松弛 节点。直到 Q 空。

核心思想：基于贪心的原则。每次取出从起点到某节点最短的距离，然后再以该节点为中心 区松弛更新起点到所有节点的距离。是一个 贪心+广度优先搜索的策略

时间复杂度： O(E + NlogN) 使用优先队列优化后， 朝队列中插入复杂度为 O(N) N为节点数目。然后遍历所有节点最多 N log N , 但是其实还访问了一遍所有的边，所以加 E 为边的数量 访问边–>取点->插入优先队列

Bellman-Ford 算法

Dijkstra算法要求边权为正数，但是这个方法不要求，并且可以用来判断负环路，就是如果图中成环且总和为负，那么在没有中转数限制下转的圈越多就越小到负无穷

该方法 基本思想是 遍历每个边 e(i, j) 如果 dist(st, j) = min( dist(st, i) + w(i, j) , dist(st, i)) 。根据连接情况初始化 dist , 第一次遍历所有边，完成之后，此时的最短距离其实其中的最短距离是 中转节点不超过 1 个 时的最短距离 （也可能没中转，取决于上述 min 表达式有没有松弛成功）。那么一共有 N个节点，所以最多需要要遍历所有边 N-1 次 即可求得确定的单源到所有节点的最短距离（不是负环图时）。

当然，图是稀疏连接的，那么不可能经过每个点都中转一次才能得到最短距离。因此在每次遍历完所有边之后如果此时的最短路径没有更新边可以退出了。

同理，借助这个原理，如果他是负环图，那么即便遍历N-1次后，最短距离依然可以更低。

核心思想： 遍历所有的边，用边松弛当前最短距离。遍历的论数代表当前可能中转的最多节点数

复杂度：O(NxE) N 为节点数，E为边的数目。

如何记录最短距离对应的路径： 通过path数组来记录路径，path[i]=j表明节点 i 取得最小路径时，其最后一段走的是节点 j 到节点 i 。知道终点后，反向查找即可。例如求起点是 0 到 终点 5 的最短路径。path[ 5 ] = k 就是起点到5取最短路劲时 最后一段是 k ->5 即 0 -> k -> 5 …..

Floyd算法

用于求任意两个节点之间的最短距离。

将上述两种算法套个循环即可完成所有点之间的最短距离

但是这里记录一下 dp 的思路 复杂度其实和 B-F算法加个循环一样

设 dp[k] [i] [j] 代表最多只能经过前 k 个节点中转时的最短路径 （就是可以经过 1,2,…k节点中的一个或者多个中转） dp[k] [i] [j] = min( dp[k-1] [i] [k] + dp[k-1] [k] [j] + w(i, j) , dp[k-1] [i] [j]) 从这个 转移方程可以看出，第一项就是 正好 以 节点 k 中转时的最短路径 ，后一项就是 k 节点能中转但是我不在这儿转的最短距离。因此如果 min 选择了前者，那么就代表在 k 节点中转，没选择，k节点就没中转。

所以最外层 依旧要遍历所有节点 复杂度和上面方法套个循环一样

并查集

思想

并查集的重要思想在于，用集合中的一个元素代表集合。我曾看过一个有趣的比喻，把集合比喻成帮派，而代表元素则是帮主。接下来我们利用这个比喻，看看并查集是如何运作的。

对于一个给定的图 它有很多节点，但是部分节点是联通的，部分是不连通的。如何判断该图中有多少个联通区域呢。

1. 初始每个节点自成一派，自己是自己的祖先 ，初始联通个数为节点数目
2. 给定图中的一个边，首先判断该边的两个端点是否在一个集合中
   • 如果不在一个集合中 说明 该边的存在会将 这两个端点合并成一个集合，因此联通个数-1，并将两个集合合并，合并的思路很简单，将他们附属在同一个祖先下即可
   • 如果在一个集合中 返回false 说明这个边的存在不影响当前联通的个数
3. 这样遍历所有的边 最后就可以计算出联通图的个数

作用

并查集 简单来说有两个功能

1. 查询两个集合是否相交
   
2. 合并两个不相交的集合 需要合并所有节点

他的查询和合并时间复杂度是相互约束的。如果所有相连的节点都挂在同一个祖先下，即树的深度只有1，那么查询的复杂度为1，但是合并的复杂度就为O(N)，（因为要将一个集合的所有节点的祖先重新设置）。也可以在合并时适当控制树的深度来平衡查询和合并的复杂度。

题目背景 若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。 题目描述 规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。

public class UnionFind1 implements UF {

    private int[] array;

    public UnionFind1(int size) {
        array = new int[size];
        for (int i = 0; i < array.length; i++) {
            array[i] = i;
        }
    }

    @Override
    public int size() {
        return array.length;
    }

    private int find(int p) {
        return array[p];
    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public void unionElements(int p, int q) {
        int pID = find(p);
        int qID = find(q);
        //如果本身就是相连的
        if (qID == pID) {
            return;
        }
        for (int i = 0; i < array.length; i++) {
            if (array[i] == pID) {
                array[i] = qID;
            }
        }
    }
}

最小生成树

最小生成树就是 一个图中，使它可以完全联通的最小边的权重和。这是并查集的一个典型应用

思路

1. 将所有的边权从小到大排序
2. 从小到达取边 首先判断边的两个端点是否属于同一个集合
   • 如果是就不能使用该边，因为它的加入不会使联通数量减少，说明加入之后会使当已经加入的连接成环
   • 如果不是，那么要合并这两个点对应的集合。同时这个边也是最小生成树中的一个边
3. 遍历