A Fast Approximation of the Bilateral Filter using a Signal Processing Approach
双边滤波
和高斯滤波一样都是用周围像素的加权平均的方式来代替某个像素点的亮度。与高斯滤波不同的是,双边滤波不仅考虑了中心像素和周围像素之间的欧式距离,还考虑了像素间的差异。使得双边滤波具有保持边缘的同时又具有平滑降噪的效果。如下图。高斯滤波器在图像的任意位置采用相同的高斯核, 这种处理的缺点是在实现对图像的有效平滑的同时也模糊了边缘信息, 图像的边缘区域不能很好的保持。
由定义可以看出, 在高斯滤波的基础上双边滤波器加入了正则系数和值域权重, 双边滤波里的两个权重域的概念:空间域(spatial domain S)和像素值域(range domain R), 这个是它跟高斯滤波等方法的最大不同点。
- 在图像的平坦区域,像素值变化很小,对应的像素范围域权重接近于1,此时空间域权重起主要作用,相当于进行高斯模糊
- 在图像的平坦区域,像素值变化很小,对应的像素范围域权重接近于1,此时空间域权重起主要作用,相当于进行高斯模糊

快速双边滤波
直接计算的话,上述运算量很大 因为每个位置的 值域的 权重都得重新计算。;滤波窗口越大计算量也越大。快速算法的思想是在原本的二维图像上增加一个新的值域维度。然后使用3维卷积滤波,加速计算。下面以一个一维信号来举例。
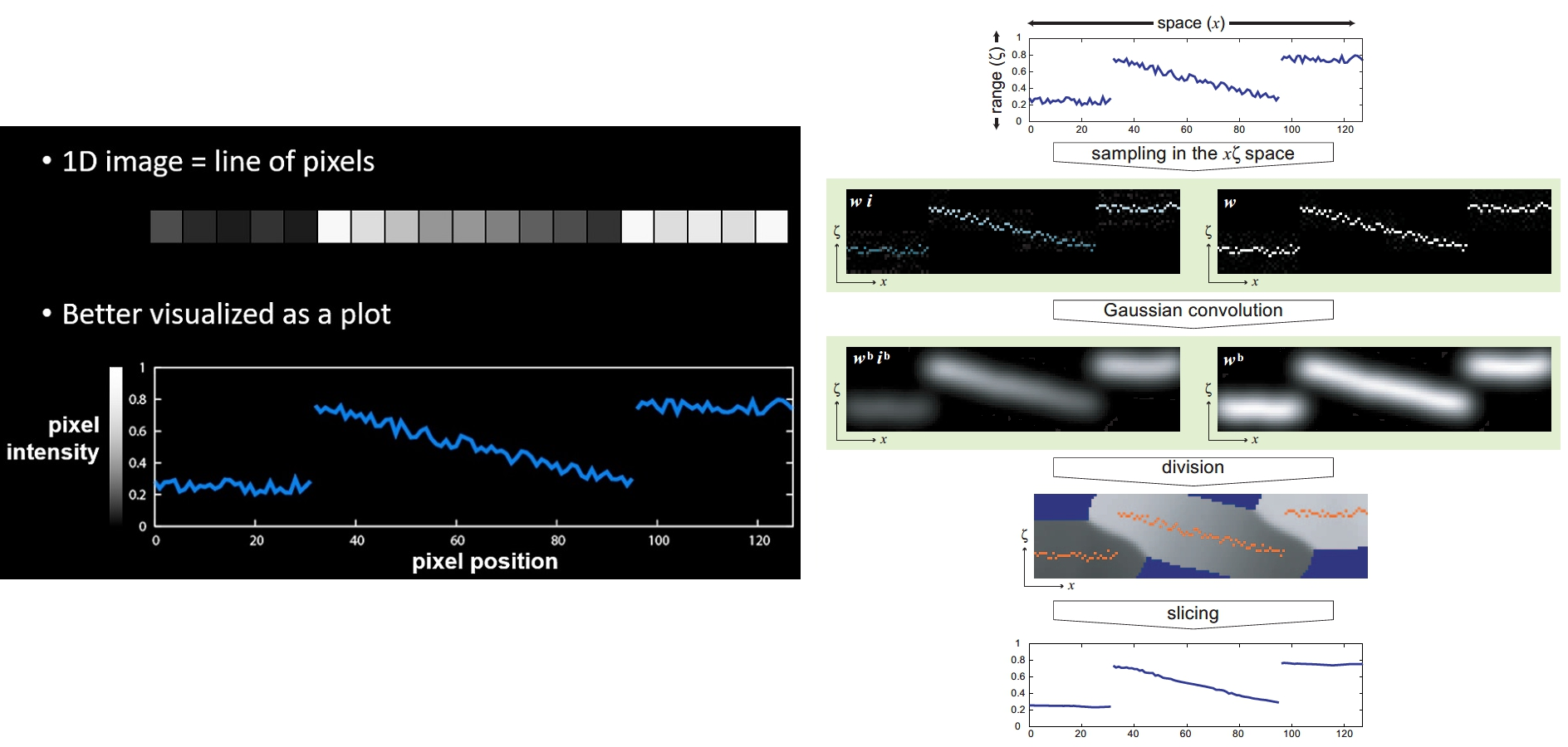
- 第一步创建双边网格。将整个网格初始化为0 。对于上右图所示的一维信号而言,如果不考虑downsample unsample sliceing的过程。将一维信号变为二维的方法就是 若原信号x位置的 值 为20,则对于 左边的wi 双边网格的 (x,y) 坐标 填充为20; 右边的w双边网格的 (x, y) 坐标位置填充 1 (为填充的位置初始为0) 这样将原始x信号依次填充 网格
- 使用一个二维高斯核 分别对 上述的wi ,w 双边网格滤波。高斯核的横轴代表空域,纵轴代表像素值域。可以 想想,原本x空域相邻的两个位置的值如果 差别很大,比如2和200,在填充双边网格时,他们在值域(图中的y轴)会被拉的很开,此时二者之间的关联在滤波核y方向的作用下被削弱甚至完全抑制。
- wi / w 做除法。之所以做除法是保证加权滤波的权重和为1。从图中可以看出在第二步滤波中,实际有很多为 0 的位置(其实就是没有像素对应的位置)也参与了滤波,因为这些为0的无效位置也占了权重,因此如果不归一化会拉低像素值。相当于 (0.5x20 + 0.3x15 + 0.2x0) / (0.5x1 + 0.3x1 + 0.2x0) 其中右边为0 的位置就是不存在像素的位置。而双边网格 i (0/1 标记有意义和无意义的位置) 的目的就是记录有效像素的滤波核的权重和。
对于二维图像,增加一个值域坐标轴 就是三维的了 过程类似。同时为了降低计算量。原文作者的双边网格其实是在较原图较小的分辨率上做的。对于在一个bin里面的很多像素取平均.... 在低分辨率下得到的双边网格最后插值的方法上采样即可。具体算法流程如下:
