From Fidelity to Perceptual Quality: A Semi-Supervised Approach for Low-Light Image Enhancement CVPR2020
DRBN
思考
值得注意的地方:
- 设计了 一个 递归的网络结构,结构比较有新意,第一阶段训练始终将特征分为三个分辨率频带,并且不同频带间使用残差学习的结构。
- 将对抗损失引入,用来提高 第一阶段 端到端学习生成图像饱和度 亮度等依然不足存在的问题。而这个对抗损失的训练又可以使用其他不配对的数据。
疑问:
- 整个结构还是在学习低光照图像到 正常光照图像间的 端到端的映射,而且 以这个方式在LOL数据集上训练 最终在其他无参考图像数据上的泛化能力如何 还未知,文章也未做对比试验。所以感觉泛化能力不行,估计不如使用retinex的网络。
- LOL数据集的成对图像本来就不适合这种端到端的学习,因为它的正常光照图像其实很多效果都不是很好(亮度不够,可能只是没有噪声),因为这个数据集的主要目低时提供不同曝光度的图像对 用于光照估计分解。所以作者不得不在第二阶段加入 一个类似对比度增强的变换网络。
- 有待在其他数据集上验证效果。
主要贡献
首先提出了一个深度(D)递归(Recursive)带(Band)网络(Network) 使用成对的 正常/低光照图像 去学习增强的正常光照图像的线性递归带表示。然后使用另一个网络来学习线性变换 提高上一阶段输出图像的视觉效果,此阶段基于 未配对的 感知质量驱动的对抗学习损失训练。
- 这是首次 提出 适用于低光照图像增强任务的 半监督学习框架,设计了 深度递归带的表示形式,来连接全监督和无监督部分 以整合他们的优点。(什么是无监督 什么是半监督?)
- 提出的框架经过精心设计,可以提取一系列粗到细的频带表示。 通过以递归的方式进行端到端训练,能够消除噪声和校正细节,这些频带表示的估计是相互受益的。
- 在质量感知的对抗性学习的指导下,深层表示被重新变换。基于平均意见得分(MOS)在感知上选择鉴别器的“真实图像”。 低光图像增强任务中的第一个试验。
主要内容
动机
Recursive Band Learning paired 成对的图像数据 可以对图像细节增强提供强大的约束。所以第一阶段,基于 成对的训练数据的约束,使用 深度递归带 (这里的带 应该代表频带,表示不同分辨率的特征图/图象) 网络 来恢复重建图像的细节信号。这一阶段不仅从输入图像 y 中 生成了最终增强图像 \(\hat{x}=\sum_{i=1}^{n} \hat{x}_{s_{i}}^{T}\) ,还生成了 一系列分辨率的特征带 \[\left\{\Delta \hat{x}_{s_{1}}^{T}, \Delta \hat{x}_{s_{2}}^{T}, \ldots, \Delta \hat{x}_{s_{n}}^{T}\right\}\] 通过对成对的低光/正常光数据进行完全监督来学习 \(\Delta \hat{x}_{s_{i}}^{T}\) 。
连接递归带的特征和对抗学习。但是,第一阶段的首要目的是尽可能恢复信号细节,自然无法获得良好的视觉质量。因此这一阶段对第一阶段学习的 信号带进行重建,来获得更符合人类视觉效果的更好的结果。如下式:
\[\hat{x}=\sum_{i=1}^{n} w_{i}\left(y,\left\{\Delta \hat{x}_{s_{1}}^{T}, \Delta \hat{x}_{s_{2}}^{T}, \ldots, \Delta \hat{x}_{s_{n}}^{T}\right\}\right) \Delta \hat{x}_{s_{i}}^{T}(y)\]
上式可以看出 ,首先这阶段的网络输入是 上一阶段生成的几乎无噪声的,细节很好的图像,输出获得具有更好光照更好对比图的图像。网络学习的是变换参数。
网络结构
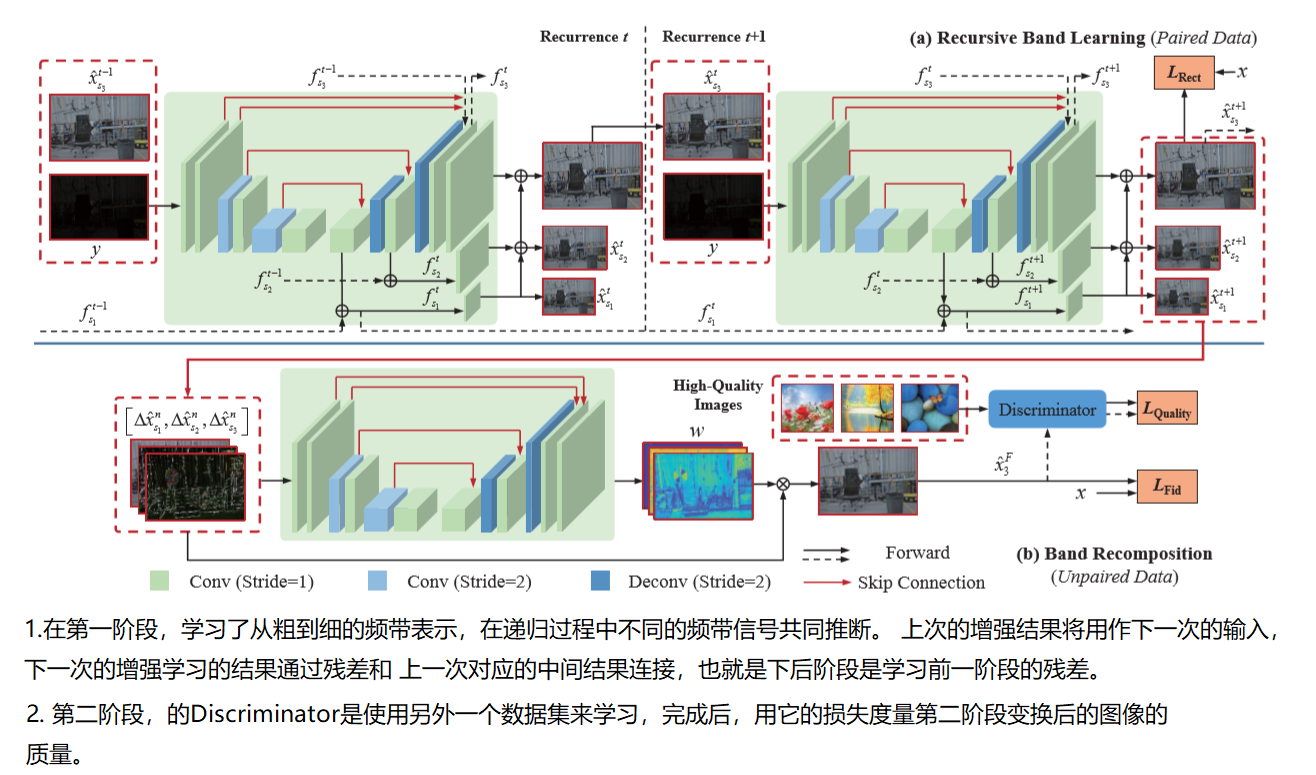
Recursive Band Learning
这一阶段使用一系列 U-NET类似的网络结构(BLN)来完成迭代。图中的分辨率分别为 1/4, 1/2,1 。首先输入图像y经过一个BLN_F 生成 。f 为每个网络生成的中间特征,有不同分辨率的 和上一轮生成的 f 求和 生成当前层的 x 输出,其次也会直接输入下一层 和下一层的 f 求和。这样以来 每次递归的其实是 学习的 上一轮 生成的 f 的残差。所以说由粗到精细特征。
\[\begin{aligned} \left[f_{s_{1}}^{1}, f_{s_{2}}^{1}, f_{s_{3}}^{1}\right] &=F_{\mathrm{BLN}_{-}}^{1}(y) \\ \hat{x}_{s_{1}}^{1} &=F_{\mathrm{R}_{-s} 1}^{1}\left(f_{s_{1}}^{1}\right) \\ \hat{x}_{s_{2}}^{1} &=F_{\mathrm{R}_{-s} 2}^{1}\left(f_{s_{2}}^{1}\right)+F_{\mathrm{U}}\left(\hat{x}_{s_{1}}^{1}\right) \\ \hat{x}_{s_{3}}^{1} &=F_{\mathrm{R}_{s_{3}}}^{1}\left(f_{s_{3}}^{1}\right)+F_{\mathrm{U}}\left(\hat{x}_{s_{2}}^{1}\right) \end{aligned}\]
接着是中间层的 不断 递归迭代。输入为 y 和上一层增强的输出。中间层的递归网络学习的都是前一层的 残差
\[\begin{aligned} \left[\Delta f_{s_{1}}^{t}, \Delta f_{s_{2}}^{t}, \Delta f_{s_{3}}^{t}\right] &=F_{\mathrm{BLN}_{-} \mathrm{F}}^{t}\left(y, \hat{x}_{s_{3}}^{t-1}\right) \\ f_{s_{i}}^{t} &=\Delta f_{s_{i}}^{t}+f_{s_{i}}^{t-1}, i=1,2,3 \\ \hat{x}_{s_{1}}^{t} &=F_{\mathrm{R}_{s} s_{1}}^{t}\left(f_{s_{1}}^{t}\right) \\ \hat{x}_{s_{2}}^{t} &=F_{\mathrm{R}_{s} s_{2}}^{t}\left(f_{s_{2}}^{t}\right)+F_{\mathrm{U}}\left(\hat{x}_{s_{1}}^{t}\right) \\ \hat{x}_{s_{3}}^{t} &=F_{\mathrm{R}_{s} s_{3}}^{t}\left(f_{s_{3}}^{t}\right)+F_{\mathrm{U}}\left(\hat{x}_{s_{2}}^{t}\right) \end{aligned}\]
最后是 损失函数。可以看出,它是 分别计算在分辨率 s=1 /2 1/4下的SSIM损失 FD为下采样。
\[\begin{aligned} L_{\mathrm{Rect}}=-&\left(\phi\left(\hat{x}_{s_{3}}^{T}, x\right)+\lambda_{1} \phi\left(\hat{x}_{s_{2}}^{T}, F_{D}\left(x, s_{2}\right)\right)\right.\\ &\left.+\lambda_{2} \phi\left(\hat{x}_{s_{1}}^{T}, F_{D}\left(x, s_{1}\right)\right)\right) \end{aligned}\]
上述的设计有以下好处:
- 上一次迭代生成的高频带将会对这次迭代的低频特征的生成产生影响,因为这次迭代的输入是上一次生成的的高频带特征 S3 和 y的组合。而最终的损失也是高低频带分别计算,所以高低频带之间的连接是相互影响的,双向流动的。
- 递归学习增强了建模能力。 后面的重复仅需要恢复残差信号,并以先前重复的估计为指导。 因此,可以获得准确的估计,只需将更多的注意力放在细节的恢复上。
Band Recomposition
借助配对数据的约束,可以很好地学习从弱光图像到正常光图像的波段恢复过程,同时可以很好地恢复细节并抑制噪声。 由于信号保真度始终无法很好地与人类的视觉感知保持一致,尤其是对于图像的某些全局属性(例如光线,颜色分布)。因此这一部分的目的就是 对上一阶段的频带信号重建,得到视觉效果更好的图像。
首先 可以看出 左半部分还是使用一个UNet结构的网络来学习变换的参数,使用生成的参数对 原始频带型号线性变换。得到新的生成图像,使用 对抗损失 和 SSIM/VGG 损失共同优化网络。而对抗损失 是使用 另一个数据集学习的用于度量图像频分的一个网络 SSIM/VGG损失都是 需要输入的参考图像作为约束的损失。因此这一部分的UNet训练也是需要LOL数据集的,只是对抗损失网络是使用其他不成对的数据训练的。 损失函数:
\[\begin{aligned} \left\{w_{1}, w_{2}, w_{3}\right\} &=F_{\mathrm{RC}}\left(\left\{\Delta \hat{x}_{s_{1}}^{T}, \Delta \hat{x}_{s_{2}}^{T}, \Delta \hat{x}_{s_{3}}^{T}\right\}\right) \\ \hat{x}_{3}^{F} &=\sum_{i=1}^{3} w_{i} \Delta \hat{x}_{s_{i}}^{T} \\ \Delta \hat{x}_{s_{i}}^{T} &=\hat{x}_{s_{i}}^{T}-F_{\mathrm{U}}\left(\hat{x}_{s_{i-1}}^{T}\right), i=2,3 \\ \Delta \hat{x}_{s_{1}}^{T} &=\hat{x}_{s_{1}}^{T} \end{aligned}\]
\[\begin{aligned} L_{\text {Detail }} &=-\phi\left(\hat{x}_{3}^{F}-x\right) \\ L_{\text {Percept }} &=\left\|F_{\mathrm{P}}\left(\hat{x}_{3}^{F}\right)-F_{\mathrm{P}}(x)\right\|_{2}^{2} \\ L_{\text {Quality }} &=-\log D\left(\hat{x}_{3}^{F}\right) \end{aligned}\]
其中 D 是 估计 生成图像符合人眼视觉效果的概率,这个D是在
high-quality images selected from aesthetic visual analysis dataset
这个数据集上训练的。Fp是VGG损失。
实验
训练细节
首先使用 LOL 上成对的数据 先训练第一阶段的网络,然后固定第一阶段 的权重 再训练第二阶段。具体训练方法如下:

实验结果
