常见的面试题

记录了CS-NOTE中整理的高频面试题，把不会写的单独记录下来了

数组中的重复数字

这道题可以用判断环的方法找环的起点
通过swap的方式 swap(nums[i], nums[nums[i]]) 将数组还原为 num[i] = i 若遇到 num[i] == nums[nums[i]] 则为重复的数字。

二维数组中的查找

类似双指针的使用方式之一，不过不是二分查找，而是设置行列指针，选取矩阵右上角为起点，这样行指针往左移，列指针往下移，数据分别边小，变大。核心思想就是两个指针都是单方向移动，且指向的数据变化趋势是相反变化的，这样依次判断和target的大小关系只能有一个放行的指针移动。

替换空格

主要在于如果只能在原字符上操作，首先遍历判断空格数量，将源字符串扩容 + i x 2；接着从字符串末尾两个指针，依次从后向前填充。例如原本 “ss ss” ->“ss ss ”

二叉树的下一个结点

1. 该节点没有有子节点。当它有右子节点时，中序遍历接在它后面输出的节点应给是它子树的最左边的叶子节点

        2. 该节点没有子节点。这时就要回溯了，一直找到它父节点，知道它是父节点的左子树为止。 具体要参照中序遍历的输出规律。好理解

矩形填充

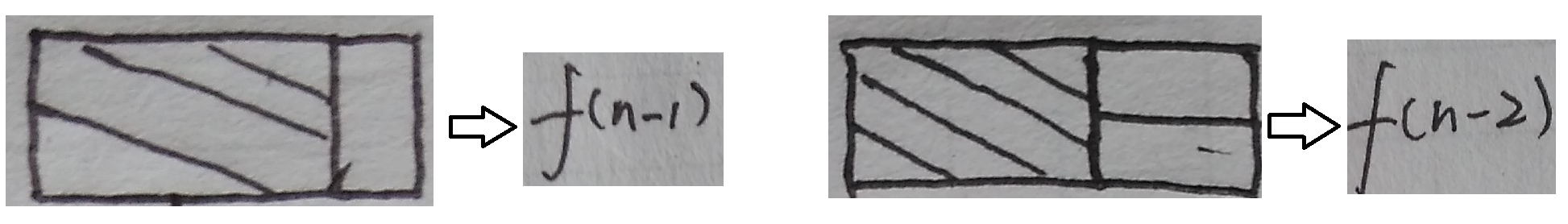
f(n) = f(n-1) + f(n-2) 斐波拉西

青蛙跳台阶

这个和上一道一样，状态方程在于看青蛙最后一步是跳一步还是最后一次一下子跳两步，就转换为斐波拉西数列。最后(a + b)%c = (a%c + b%c)%c。

矩阵中的最小路径

考点是回溯算法，使用深度优先遍历实现回溯。回溯和单纯的优先遍历的区别在于回溯在每次试探性的前进之后有条件判断剪纸。如果沿着某一方向下去不满足条件马上返回，并且需要还原之前的状态

机器人的运动范围

这题就套用DFS BFS模板即可

数值的整数次方

这个题考察的是快速幂乘法，a^N = axaxa…xa 这样直接一个个乘肯定是很慢的，会超时。将N 转换为二进制表示。如N = 9，则a^9 = a^(1001) = a^{(1x8+0x4+0x2+1x1)} = a¹ x a^0x2 x a^0x4 x a^1x8 ; 循环计算 a = a*a；即计算了 a⁰ a² a⁴… 对于N的二进制为1的位置就乘进结果，为0 的就乘1。

动态规划。f[i] [j] 表示字符串 s (目标字符串) 的前 i 个字符和 p (正则字符串) 的前 j 个字符匹配的状态。那么对于 f[i] [j] 当 p[j] 不是 “*” 时就很简单只用看 i-1 j-1 的状态和 s[i] 与 s[j] 是否匹配（相等或者为‘.’）即可。复杂的是当 p[j] 为※号时的情况。如果 ※号的用法可以分为两类： 1. 他前面一个字符出现0次，就是消掉他，那么 f[i] [j] 的状态由 f[i] [j-2]决定。 2. ✳将他前面的字符重复1-n次的情况。此时若 s[i] 和 p[j-1] 匹配,例如都等于a，那么就由 f[i-1] [j] 状态决定，此时相当于 s[i-1] 后面再加一个 a 此时 ✳再复制一次即可所以状态取决于 f[i-1] [j]

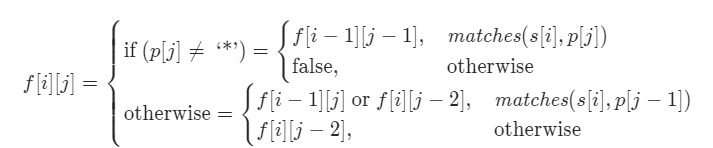
删除链表倒数第K个节点

核心的使用快慢指针先将快指针从头往后移动K个，再二者一起往后移动，知道快指针为NULL 责慢指针停下的地方就是了。为了排除边界情况可以在链表头加一个哑铃节点，然后每次让慢指针停在待删除节点的前一个节点。这样就不用备份慢指针的父节点啦。

链表反转

双指针，两个相邻的指针，每次反转一个。一个初始化为NULL 另一个为头指针
递归 / 栈

合并两个有序链表

递归！！！！

顺时针打印矩阵

使用的深度优先遍历 + 减枝速度较慢。反正都是暴力

包含min函数的栈

要求O(1)的时间复杂度取出栈中的最小值（不是每次都删除最小值），使用一个辅助的栈来将最小的保存在栈顶。当push进一个数时，如果比当前栈顶最小的小那么就进入这个辅助栈….. 单调栈

栈的压入、弹出序列

用一个栈模拟出栈操作，如果最后栈空，则OK。首先读取push数组中的一个数，并加入堆栈，如果它和pop数组中的数相同，则马上将其出栈，并将 push 数组指针滑动。

二叉搜索树的后序遍历序列

    1. 递归  分治法。抓住 后续遍历 和  搜索树的特点

        2. 单调栈

二叉树中和为某一值的路径

前序遍历先判断是不是和满足要求且到达叶子节点是这里的技巧可以在遍历完左右子节点后再将当前节点的值出栈。这样不用来回拷贝vector 省时间

复杂链表的复制

Hash表保存每个节点和新new的节点的对应遍历两编链表第一遍 new 拷贝所有节点并 map 第二次遍历链接节点

二叉搜索树与双向链表

首先二叉搜索树 -> 有序双向链表。就能想到中序遍历。暴力的方法是，首先中序遍历将所有节点存下来，然后链接。也可以在中序遍历的时候进行指针的转换，这样只用遍历一次，而这样的难点就是如何在中序遍历中转换指针的指向。申请两个节点指针，pre 和 cur pre指向上一次遍历指向的节点，cur为当前遍历指向的节点。初始 pre 初始为 dummy指针。在中序遍历的位置完成 pre 和 cur 左右节点的指向，同时更新 pre 的指向：（可以看出在中序遍历回到节点时，此时已经完成左子节点的遍历，因此左指针可以修改。此时也确实只修改了左指针）最后使用dummy指针找到节点头。最后的cur指针指向的是最后一个访问的节点，即节点的尾。

       dfs(root->left);
cur = root;         // 变更开始时更新 cur
pre -> right = cur; // 变更左右指针的指向， 符合双向链表的指针指向， 即当节点有一个指针指向前一个节点， 前一个节点也有一个指针指向当前节点
cur -> left = pre;
pre = root;         // 变结束后更新 pre ， 以便下一次使用
dfs(root->right);

数组中出现次数超过一半的数字

使用Hash法空间复杂度O(N) 时间复杂度 O(N) 由于题目说某个数字的个数出现次数大于一半，那么可以使用一个计数变量，当遇到相同的数字+1 否则-1 当减为负，这个数字就是当前遍历的中最多的。而遍历完，这个指向数字一定是最多的。

最小的k个数](https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/)

这道题的考点是快排中分治的思想或者优先队列（二叉堆）。二叉堆的基本性质是堆顶元素 top 总是最大/最小的。因此构建一个含有K个元素的优先队列，依次读取剩下的元素，若比堆顶小，则弹出堆顶元素并将新元素入堆…. 类似解决 topK 的题都是这两种思路最好。快排的思想是当前选取一个基准数，然后比他大的和小的各放一边…..

数据流中的中位数

    1. 第一中方法是 每次插入 都保持 数组有序，使用二分法插入元素。取中位数的时候 就直接取中间即可。查找O(logn) + insert(O(n)) =插入新数据一共 O(n)。

        2. **使用优先队列的方式**。构建一个大顶堆和一个小顶堆。大顶堆保存中位数左边较小的 数据，小顶堆保存中位数右边较大的数据。每次插入新数据，先将其加入大顶堆，再将大顶堆的最大数据弹出 加入小顶堆；然后判断一下两个堆的大小，保证大顶堆的数据量>小顶堆的。求中值的时候，奇数个数据就是 大顶堆数据 最大的那个 4，3  偶数二者平均。 加入新数据 时间复杂度 O(logn)

class MedianFinder {
    priority_queue<int> lo;                              // 大顶堆
    priority_queue<int, vector<int>, greater<int>> hi;   // 小顶堆

public:
    // Adds a number into the data structure.
    void addNum(int num)
    {
        lo.push(num);                                    // 加到大顶堆

        hi.push(lo.top());                               // 平衡
        lo.pop();

        if (lo.size() < hi.size()) {                     // 维护两个堆元素个数
            lo.push(hi.top());
            hi.pop();
        }
    }

    // Returns the median of current data stream
    double findMedian()
    {
        return lo.size() > hi.size() ? (double) lo.top() : (lo.top() + hi.top()) * 0.5;
    }
};

数字 1 的个数

这是个找规律的题目

把数组排成最小的数

排序对于相同长度的字符串，直接从高位到低位，小的字符排在前面。对于不同长度的字符串a, b 比较 a+b b+a 大小即可。就是正反组合产生的新的字符的相互比较。

把数字翻译成字符串

动态规划

礼物的最大价值

动态规划二维dp 每个位置的最大礼物价值只由它的左边和上边格子的最大数的较大者决定。

丑数

首先，判断一个数n是不是丑数，就看 n能否被分解为多个 2 or 3 or 5 相乘的形式。

while(n!=1){
	if(n%2==0) n/=2;
	else if(n%5==0)	n/=5;
	else if(n%3==0) n/=3;
     else return false;
}

但是要输出第n个丑数，暴力遍历从1开始的所有整数计算是否为丑数然后累加到n停止，虽然可以使用备忘录的方法加速计算，即如果 k/2 为丑数那么 k 也为丑数，但是依然会超时。

数组中的逆序对

使用归并排序的方法。分治的思想。在归并排序中，每次将数组划分为左右两半部分分别 sort 然后再 merge 。

class Solution {
public:
    int cnt = 0;
    void mergeSort(vector<int>& nums, vector<int>& tmp, int lf, int rt){
        if(lf >= rt)     return;
        int mid = (lf + rt) / 2;
        mergeSort(nums, tmp, lf, mid);   //递归的调用归并排序  排序后  左半部分 和 右半部分都是有序的
        mergeSort(nums, tmp, mid+1, rt);
        int pos = 0;
        int i = lf, j = mid+1;
        while(i <= mid && j <= rt){   // 双指针将两个有序的 左右半部分合并为一个有序的数组，此时需要一个缓存数组 tmp
            if(nums[i] <= nums[j]){
                tmp[pos++] = nums[i++];   
            }else(nums[i] > nums[j]){
                cnt+=mid-i+1;            //  相对归并排序增加的一个计数变量  
                tmp[pos++] = nums[j++];  
            }
        }
        while(i<=mid){
            tmp[pos++] = nums[i++];
        }
        while(j<=rt){
            tmp[pos++] = nums[j++];
        }
        for(i = lf; i <= rt; i++){  // 将tmp的内容再存储到num中
            nums[i] = tmp[i-lf];
        }
    }
    int reversePairs(vector<int>& nums) {
        vector<int> tmp(nums.size());
        mergeSort(nums, tmp, 0, nums.size()-1);
        return cnt;
    }
};

两个链表的第一个公共节点

这个题暴力的是查询的算法，但是时间空间复杂度较低，最好的是双指针算法。两个指针分别从A,B开始遍历，到达终点后就换个起点接着遍历。最终二者相遇的地方便是交点.

数组中数字出现的次数

这个题用异或做异或的性质

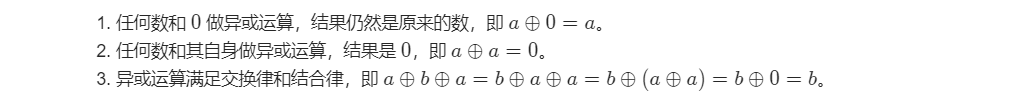
如果对于一个数组只有一个数字出现了一次,其他数字都出现了两次，找出这个单独的数字。根据异或的性质，全员异或最终的结果便是这个单独的数字。而此题是有两个不同的单独的数字，要找出这两个。最直观的想法是，将这两个不同的数字分别放在两组，然后每组中除了这个单独的数字就是其他成对的数字，这就退化成了第一个问题。即要求分组的数字有以下性质：

两个不同的数字分别被分到不同的组
每组中除了一个不同的数字其他的都是成对的这样组内全员异才能满足最终的结果是不同的那个。

如何分组？首先全员异或，结果肯定是两个不同的数字异或的结果。而这两个数字异或结果为1 的位代表这两个数字该位不同，一个为1 另一个必定为0。例如 011 111 异或， 100 则第三位肯定不同。这样根据该位的值来分组可以很好的分开这两个数字到不同组，对于其他数，相同的该位也一定相同，也一定在一个组。由此两个条件都满足。所以这样分组，再组内异或分别就找出了两个不同的单数字。

而解决此类除了除了某个元素出现一次其余均出现 m 次的问题 都可以统计二进制各个位元素为1的个数，如果个数 % m 有余数，那么表明该位是不同的那个数字为 1 的位置。

平衡二叉树

滑动窗口的最大值

这道题考察有序队列。实现有序队列要结合 c++ 标准库中的 deque 双端队列，即可以从前也可以从后插入删除数据。对于队列，如果后进去的数据比我队列尾端的数据小，就直接放在它后面，如果比他大，就将原本尾部的数据弹出，直到遇到比他大的数据，再将其放进去。这样队列头部一定是当前队列的最大数据。删除的时候，只用判断当前要出对队的元素是不是和头部的相同，相同就弹出。

class MyQueue { //单调队列（从大到小）
public:
    deque<int> que; // 使用deque来实现单调队列
    // 每次弹出的时候，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出。
    // 同时pop之前判断队列当前是否为空。
    void pop (int value) {
        if (!que.empty() && value == que.front()) {
            que.pop_front();
        }
    }
    // 如果push的数值大于入口元素的数值，那么就将队列后端的数值弹出，直到push的数值小于等于队列入口元素的数值为止。 
    // 这样就保持了队列里的数值是单调从大到小的了。
    void push (int value) {
        while (!que.empty() && value > que.back()) {
            que.pop_back();
        }
        que.push_back(value);

    }
    int front() { // 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
        return que.front();
    }
};

n个骰子的点数

直接动态规划或者递归+dp备忘录减枝 (因为直接递归有大量的重复计算)

圆圈中最后剩下的数字

首先，考虑一种规律。对于一个圈不管起点是从哪个点开始，假设是 2，最终最后一个留下的是第3个，那么如果此时开始的位置为3，那么最后剩下的位置就是 4 （此时不考虑成环返回的问题），因为其实所有数字围成一个圆圈，处处堆成，起始位置和最终位置肯定是保持一个相对的位置关系。

如果假设 f(n-1, m) = x 代表第n-1个数，从0开始，m个删除一次，最终剩下的数的位置是 x；考虑 f(n, m) 的关系。n个数，在第一次删除，即去掉第 m -1 个数后(起点是从0开始)，就剩下 n-1 个数了，此时就退化为 f(n-1, m) 了只不过，这里n-1的起点是 m%n （删除了第 m%n-1个数，就从第m%n个数开始）。根据上面的规律，f(n, m) = (x + m%n) % n。起点相对 f(n-1) 的 0 变为 m 终点也应该相对 x 向后 + m，由于是环，所以 % n

求1+2+…+n

判断，循环语句等不能用。使用递归求和但是需要有判断递归停止的条件，可以使用 && 逻辑运算符 替代判断。当递归的返回值 n 为 0 就开始 return

class Solution {
public:
    int sumNums(int n) {
        n && (n += sumNums(n-1));
        return n;
    }
};

不用加减乘除做加法

使用位运算比较简单

计算机中申请一个 int 型的变量，它在内存中直接存的补码。因此此题只用将两个数按照加法的逻辑计算即可，不需要再转补码了。

位运算两个数相加可以分为两部分：无进位和 + 进位满足以下规律：

class Solution {
public:
    int add(int a, int b) {   //当进位 为  0 时 就停止递归 计算结束
        return b ? add(a^b, (unsigned int)(a&b)<<1) : a;
    }
};

Ruowang's blogs