记录了动态规划类的题目

动态规划类题目

连续子数组问题

连续子数组问题要充分利用连续这个条件。连续子数组（区间和）也可能是前缀法求解的题

等差数列划分

关键是对于一个等差数列例如 -1, 0, 1, 2, 3 这个数列第2个开始等差子数列个数为 1 依次为 2+1=3 3+2+1=6 可以理解为当只有三个元素时子序列就只有他本身1个，当有四个元素时，子序列总个数分为以下两部分（含有三个元素的子序列个数 + 含有四个元素子序列的个数）前者就为上一次的个数 + 1 后者就为上上次的个数。以此类推如若有五个元素的等差数列那么子序列的个数就为 3 + 2 + 1 （三个元素的，四个元素的，五个元素的子序列）所以 dp[i] = dp[i-1] +1 ; all_cnt = dp 求和（非等差序列的位置的dp = 0）

连续子数组和

基本方法是积分法，记录每个位置的前面所有元素和。基于此将子区间的所有元素求和转化为求差，两元素的差等整除K 就相当于两元素对k的余数相同。判断相同这里用了哈希表的方法。 (sum(i) - sum(j) ) % k= sum(i~j) % k = 0 => sum(i) % k == sum(j) % k

相邻元素状态转换

1股票交易类问题，我们这一次买还是卖只跟上一次我们卖还是买的状态有关，例如前一天刚卖股票，有个冷冻期，那么今天就不能再买。
打家劫舍类问题。上一个元素的选择与否关系到当前元素的选择与否。通俗的理解可以将状态值设置为上一个元素是否选择，那么状态数组就为 dp[n] [2] ，这么理解就和买卖股票类的问题相通了。
非典型的，上一个元素的操作关系到当前元素的操作；使序列递增的最小交换次数，当前元素的交换与否只与前一个元素是否交换有关。他们的本质都是： dp[n] [k]，其中 n 为序列数组的长度，k 为当前操作的状态数，为1，2或者3…
题目本身可能不会很明确告诉你相邻元素的转换关系，例如删除并获得点数

母牛生产

假设农场中成熟的母牛每年都会生 1 头小母牛，并且永远不会死。第一年有 1 只小母牛，从第二年开始，母牛开始生小母牛。每只小母牛 3 年之后成熟又可以生小母牛。给定整数 N，求 N 年后牛的数量。

一只小牛在三年成熟之后可以每年开始产一头小牛。那么第 dp[i-1] 表示第 i-1年的小牛数量首先它可以顺延至 i 年因为不会死。其次这其中还有一批牛已经是成熟的母牛可以每头再产一头小牛，那么 i - 1中有多少头成熟的小牛呢，因为小牛变成成熟母牛需要三年，那么第 i 年往前推3年的 dp[i-3] 第 i-3 年的牛到第 i 年隔了三年，也即是 dp[i-1] 年的牛每头可在 i 年产一头小牛即第 i 年牛的数量是 dp[i] = dp[i-1] + dp[i-3]

删除并获得点数

主要思想是构建上面那个 all数组，就将状态转移函数简化了很多。all数组的含义是对数组中的每个整数元素的计数，数组的下标代表元素i 。例如 all[1] 代表数组中元素1 的个数。如果没有则为0。这样 dp 的每个状态的切换只在相邻的两个下标发生，dp[i] 与 dp[i-2]没有关系。这样简化了状态转换的情况。

使序列递增的最小交换次数

这个题的关键在于每次只能交换相同位置的两个元素。当交换求前n个元素最小交换次数的时候，只需考虑前面两个元素时候交换，并且对应的交换次数。这么一来就会有四种情况，两两取最小。1. 上一次没交换，这一次也不交换，总交换次数不变 2. 上一次交换了，这一次不交换；3. 上一次不交换，这一次交换； 4. 上一次交换，这一次不交换。1,2 3,4分别取较小值，并保存用以下一次迭代。

打家劫舍 III

打家劫舍 II

最佳买卖股票时机含冷冻期

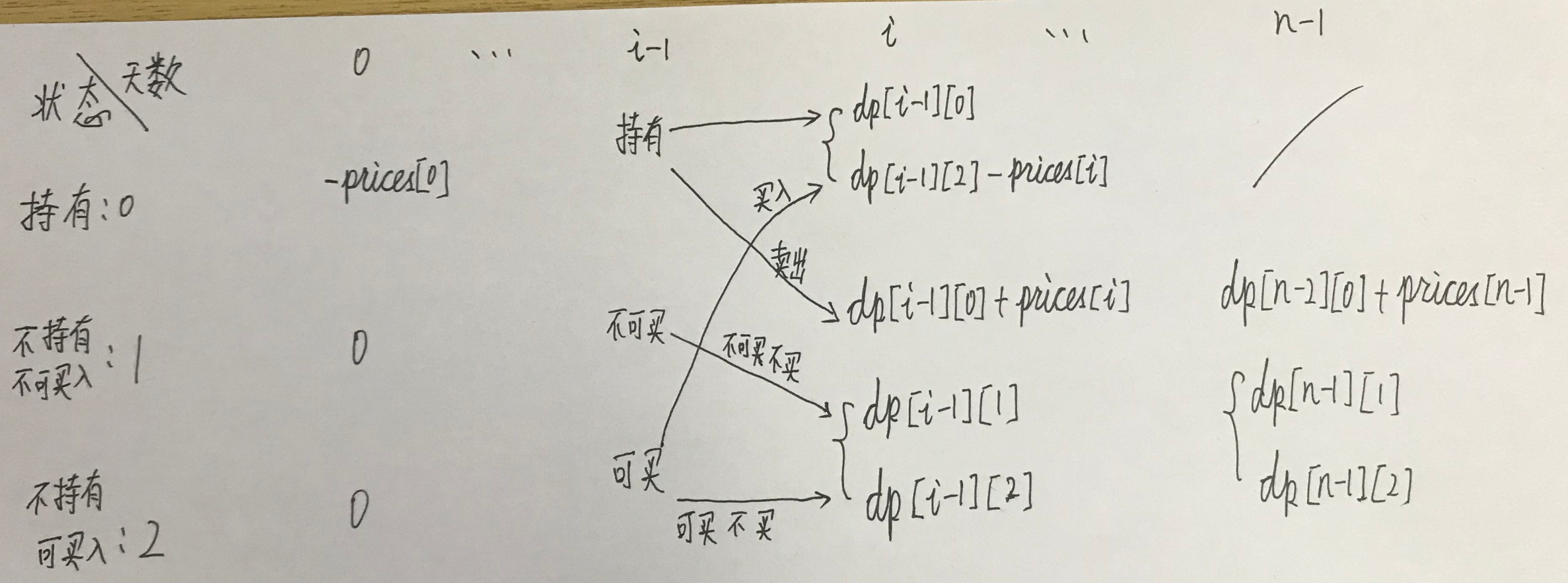
dp[i] [0] dp[i] [1] dp[i] [2] 分别代表当天持有股票时的累计财产，当太难不持有且不可买入时的累计财产，当天不持有但是可买入时的财产。理清从前一天到今天的状态准换关系即可。买入/卖出是动作，而持有不持有才是状态，由不同的动作，导致每天不同的状态，因此要以状态设置数组。

买卖股票的最佳时机含手续费

类似上

买卖股票的最佳时机 III

买卖股票的最佳时机 IV

给 N x 3 网格图涂色的方案数

青蛙过河

背包问题

这类问题通用的寻找 dp 的方法都是将目标值/背包容量设置为一个维度，按照物品列表再设置一个维度。例如零钱兑换中，要凑够 N 元，N元就是目标值（容量值），那么dp 的设置就为 dp[n] [c] ，使用前 c 个硬币凑够 n 元的方法数。背包类问题总结

组合问题：组合问题就是给定一个目标数，希望找到凑出这个目标数的所有方法。这类题就要注意题目意境中是排列问题还是严格的组合问题，如果是排列问题那么就允许 1 2 1 1 1 2 两种情况的存在。在青蛙跳台阶、解码方法的问题中就是排列，这是两种不同的方法，但是在零钱兑换 II 中这就是相同的，不能计入总数，因此一维度的dp求出来一定有重复。
- 零钱兑换 II 组合总和 Ⅳ 目标和解码方法爬楼梯
True, False 问题：不用考虑重复问题，对于分割等和子集问题，其实就可以间接的转化为凑出目标和问题，判断能否凑出该 sum / 2 即可。
- 单词拆分分割等和子集
最大最小问题：其中一零和问题是一个二维的背包问题，就是他的容量由两个维度1/0共同决定，因此它的最终状态就是 dp[] [] [] 三维数组

完全平方数

分割等和子集

记录两个思路一个是自己想到的按照回朔 + 记忆的方法一个是看解答的标准的动态规划的思想。首先无论怎么做要判断能不能分割为两个和相等的子集就是先求和然后除2 即为在数组中找和为 target的组合。

思路1，对于数组，每个元素有取和不取两种状态。因此回溯就是从前往后对于第第 i 个元素 return dfs(i， target-num[i]) | dfs(i, target) 前者是第 i 个元素取得情况下能够满足，后者是第 i 个元素不取的情况下能否后面能否满足和为 target。但是直接这样写会超时，因为会有大量重复的情况。为此加入备忘录设置 dp[i] [target] 记录子问题的结果防止重复。这种由于递归的子问题就是 dfs( i, target) 所以在加入记忆优化也必然是使用 dp 数组存储对应组合的状态，防止后面重复。

思路2，动态规划 dp 数组的含义 dp[i] [j] 表示在数组的前 0~i (包括i) 中，能否找到取和为 j 的情况。最终就是要求 dp[n-1] [ target] 的状态。考虑一下要求对于前 i - 1 个增加了第 i 个元素可以分为取了第 i 个和没取第 i 个元素。dp[ i - 1 ] [ j - num[i]] || dp[i - 1] [j] 两种取或不取。意思是如果第 i 个取了和为 j 成立那么反过来抛去第 i 个元素，前 i -1 个元素任取应该能找到和为 j-num[i] 的情况，再取一次 num[i] 就可以满足 j ；那么如果这次 i 没取但是和为 j 的情况很好理解没取相当与不存在，考虑 i - 1 的情况即可。但是还得考虑 j - num[i] < 0的情况，此时 num[i] 肯定不能取，因为已经大于 j 目标值了，所以此时 == dp[i-1] [j]。

目标和

这个题技巧和上面一样。自己做的时候先想到的不是动态规划是递归+剪枝也不会超时。单纯的暴力递归复杂的指数级，会超时。

递归的思路。首先每次选择 target - num[sel] 或者 target - num[sel] 递归。判断到最后一个元素且target==0的时候计数。剪枝的方法是，增加一个当前剩余元素的最大和limit 起始 limit = sum(nums) , 递归时 limit - nums[sel] 。通过判断当前 target 是否在区间 [-limit，limit] 之间，不在就返回不递归。

动态规划的方法。首先状态数组含义和上面题一样只不过这里记录的是个数。dp[i] [j] 的含义就是前 i 个元素的和为 j 的个数。最终就是求 dp[n] [S] 那么第一个元素就已知了 dp[0] [ num[0] ] += 1, dp[0] [-nums[0]] += 1; 那么怎么挨着求到最后呢。首先 j 的范围肯定在正负 sum( nums )之间，因此就建立一个这么宽的状态表（这样 j 的值是稀疏的，不会取到这里面的所有值）但是这么建立表格方便循环。没用到的计数值为 0 即可。虽然看起来增加了很多无用的 j 的计算过程但是相对递归的指数级时间复杂度还是好很多。状态转移就是 dp[i] [j] = dp[i-1] [j - nums[i]] + dp[i -1] [j + nums[i]] 注意数组索引正负的问题和后面溢出判断的问题。

一和零

这个题也可以看成背包问题。将每个字符串价值看成1，每个字符串占用的体积即为 0/1 数量。背包的容量为最多容纳的0/1的个数。状态 dp[i] [mc] [nc] 的含义是只有前 i 个字符串时，背包容量 (总的0/1个数) 是 mc nc 时最多可选的字符串的个数。 dp[i] [mc] [nc] = max( dp[i-1] [mc - mi] [nc - ni] + 1, dp[i-1] [mc] [nc]) 含义是这次选则第 i 个字符串，则可以取得最大数量，就是上一次最大容量为 mc-mi nc-ni 时可以取的最大个数 + 1，另一种情况是这次不取第 i 个元素，二者取大的。

零钱兑换

这道题和面试题一类中的矩形面积填充和青蛙跳台子的类型相似。这个题要求到兑换金额为 amount 需要的最少零钱的组合，那么组合的到最后 amount 只和 dp[amount - coins[i]] 有关，其中取最小即可。

零钱兑换 II

这个题和青蛙跳台阶很像（dp[m] = dp[m-1] + dp[m-2] 值看最后一步是跨了几层阶梯），但是又有本质的区别，青蛙跳台阶有先后顺序，总的次数实际是个排列问题，但是这个凑钱的问题是一个组合问题，1，2 和 2，1凑3是一种情况。所有状态方程不一样。

首先，是组合问题，假设硬币集合 [1, 2, 5] 那么就按照一个硬币一个硬币增加的逻辑来思考。就是所有取硬币的方式只和硬币种类有关，只有1 硬币只有1，2硬币含有1，2，5硬币这种。然后总的数量是需要凑的钱数 amount。也可以从背包问题推广到这个题，钱数是背包的容量，取得物品是硬币，只不过要刚好把背包装满。因此按照背包问题的通常方法状态 + 选择，即选择每次选不选当前的硬币，状态是凑成当前金额数的硬币取法组合。

dp[k] [j] 表示含有前k个硬币集合，取够金额 j 存在的组合组合数。那么对于只含前k-1个硬币组合的情况，组成金额 j 中的硬币含有几个硬币 k , 含有0个硬币k 就是 dp[k-1] [j - coins[k]] 个取法，含有两个硬币 k 就有 dp[k-1] [j - 2*coins[k]] … 以此类推求和。但是这个状态方程起始还可以简化。具体推导结论： dp[k] [j] = dp[k-1] [j] + dp[k] [j - coins[k]] ; 可以这么理解就是要凑成金额 j 可以分为不使用第 k 个硬币 dp[k-1] [j] 和使用第 k 个硬币 dp[k] [j-coins[k]] 这一项其实是保证了肯定取一个硬币 k,至于取了 >= 1的几个 k硬币，其实都包含在了 dp[k] [j - coins[k]] 中了。因为 dp[k] [] 这一行凑齐前面的金额其实都是使用了 >=0 个第k个硬币的。

最低加油次数

单词拆分

dp[i] 表示 s 中前 i 个字符能否被字典中的单词拆分。判断字符串是不是在字典中可以使用Hash来加快判断。有多个单词，其中在 I位置有一个是 true dp[i] 就等于true。

组合总和 Ⅳ

和零钱兑换问题2 对立这个是排列问题。

解码方法

中心扩散

这类状态转移的特点是：按照数组的起止位置建立状态 dp[st] [ed]，并按照子数组长度从小到大开始遍历，然后中心扩散 类似dp[i] [j] = (dp[i-1] [j] dp[i] [j+1])
因此这类问题的关键点是看长度为1的子数组（st == ed）的是否可能为迭代的起始边界值，例如最长回文子串，当只有一个字符时，它必然是回文，然后依次从中间向四周扩散。再例如预测赢家问题中，当只有一堆 i 石子时，先手比后手多的分数一定多 nums[i]

预测赢家

最大正方形

戳气球

正确的建模很关键。一开始做的时候，想到假设 k 位置为第一个戳破的气球最终的收益，然后遍历每个位置，取最大。第K个位置被戳破，那么剩下的就是不连续的数组，即 dp[ i ] [ k ] [ j ] + n[k] x n[k-1] n[k+1] 但是这时候就需要带断点的数组，中间维度K为断点。这样建模很不好写。

答案是设置 i j 的开区间中最大的收益，并且最后一个戳破的为 k 位置的气球，由于是开区间，而 k 是最后一个戳破的，所以 k 左边的部分和右边的部分是完全独立的两部分，建模方法就简单很多。很好的解析

记忆搜索

事实上大部分动态规划题都可以用递归+记忆的方法实现。尤其是那种很明显存在递归选择的题目，直接选择递归，复杂度指数级，运用备忘录的方法剪枝，可以加速。通常记忆搜索是自顶向下的搜索，而动态规划是自底向上的迭代。

有些题目，很难找出它动态规划的状态和地推关系，但是当回溯/递归的思路很容易想到，只不过会超时，超时的话再加上记忆剪枝即可。例如石子游戏问题石子游戏 II，预测赢家特别是前者，很难想到将 M 设置为dp数组。但是很容易顺着题目的思路写出递归的方式。dfs( st, M) 即从第 st 堆式子开始取，此时最多能取M堆，先手可以取得的式子总数。最后发现超时，简单根据动态规划入口参数设置记忆 dp[st] [M] 即可。

石子游戏 II

关键思想在于这个是反向推的，假设剩余的 n 堆石子时，先手开始取，能取得的最大的石子数，但是还要考虑此时 M 的值。想想如果此时从头往后递推的话，那么M 的取值与前面的取法息息相关，很难讨论全面。而从后往前推，就算是 M 最大为石子堆数的总数，就便利把所有的 M取值情况都算一下好了。注意：虽然 M 的取值都算了，但是并不是所有都有效的，这个由石子的总堆数决定的，例如表格给 i = 1 时，此时为剩余堆数为5 即第一堆开始，而第一堆第一M = 1为设定值，此时的算的M = 2,3,4..在石子只有五堆的情况下是无效的。那么从最后n堆开始，先手能取的最多石子数 dp[ i ] [m] 1<=m <= L(总堆数) 这是前两个for循环需要遍历的。对于特定的 i M 如果 i <= 2*M 表明先手可以一次拿完剩下的所有的即为最大 = sum[i : end] i > 2xM 则先手可以取 1<=x <=Mx2 ，有这几种取法。遍历所有x的取法，取最大为 dp[i] [m]。对于特定 1<=x <=Mx2 剩余 i - x 堆时先手取得的最大的数量那么 i 堆时的先手取得的总数为 sum_n - dp[i] [i - x]。遍历x 求最大的。

（事实上，尝试 dfs 的方法上述问题更好解决，而动态规划的方法起始很难想）

新21点

这个题目和上面类似也是反向递推。设置最终问题是最终得分不超过K 即为获胜的概率。假设当前起始总分数为 i ，那么求 dp[i] 总分已经有 i 分后获胜的概率。很显然这次总分数为由于一次抽取的数字只能是 [1, W] 由于是等概率抽取，那么 dp[i] = 1/W x (dp[i+1] + dp[i+2] + … + dp[i+W]) 。即递推公式，两次抽取获胜概率的关系。从规则可知，最终抽取总分数只能是 1 ~ （K-1+W）当得分大于等于K时不能抽了。而整个得分区间又可以分为两段。一段得分区间是（1~K-1），这段区间内的得分之后至少还能再抽一次，于是可以用到上述地推公式。另一段 K~K-1+W 此时已不能再抽，小于等于N的获胜概率为1 否则为0 是固定值。

综上可以从后往前推出 dp[0] 的概率定义并不关心你中间过程是怎么抽的分，只知道当前持有分数再抽下去最终会获胜的概率。而这个起始概率是从末尾已知，往前递推的。

错排问题

错排问题就是 1~n 个序号的元素和 1~n 个位置交替放，序号元素不能对应。关键在与 2，3 ，4，5 和 1，2，3，4 这种错排可以划分为 5 和 1 能否对应的问题。5 和1 对应放，剩下的就是 2，3，4,否则 5 和 1 不能对应放就相当于 2，3，4，5 和5， 2，3，4 元素个数为4个的错排。

信件错排问题

子序列/两个字符串问题

事实上这是一类问题的划分，解决这类字符串问题常用的套路可以归结到使用上述总结几个设置 dp 的常见方法。

对于两个字符串之间的关系问题，将dp 设置为 dp[i] [j] 以为 s 串的前i个和 v 串的前 j 个之间的最长公共子序列长度/编辑次数
单个字符串的摆动序列这种问题，就是以状态作为 dp 的第二个维度。dp[i] [k] 在 i 位置结束的子串的上升序列的长度…就类似相邻元素状态转换问题了，自己根据可能的状态设置dp数组的第二维度的含义。
字符串问题还可以设置 dp[st] [ed] 即字符串的起始结束子串，用到类似 中心扩散的原理判断回文串。
有些问题可以间接转化为最长公共子序列这种经典问题来求解，例如两个字符串的删除操作根据题意就等价于求最长公共子序列

最长上升子序列

基本的方法是动态规划法高级的是二分法+动态规划。动态规划的状态数组为第 i 个元素结束的最大上升子序列个数。那么以第 i + 1 个元素结束的最大上升子序列可能是从前 i 个结尾的任意一个接过来的因此要取最大同时从第 j 个接至第 i 个元素如 num[ j] < num[ i ] 那么 dp[ i ] + 1 否则 1 因此O(n^2)

最长公共子序列

两个字符串的删除操作

编辑距离

这个题就有意思了，按照第1种情况去假设dp数组可以解出来，但是状态转移方程可能会列的不对，原因是插入删除替换三种情况没考虑全。

摆动序列

这个题可以按照题目最长上升子序列的思路 dp设置为 dp[n] [2] 0 表示i位置结尾上升子序列的个数 1 表示下降的个数使用相同的n^2的时间复杂度循环即可。但是这个摆动序列相对那个题目可以优化，因为是摆动序列其实状态转换就只和当前元素与它前一个元素的大小关系有关再与之前的无关所以可以做线性优化 o(n) 只循环一次若当前元素大于上一元素当前元素的上升个数等于前一元素的下降个数 + 1 另一个不变…..