记录了解题中需要用贪心思路的题目。
贪心思想
这类题目往往都 有 排序?
根据身高重建队列
这道题的关键是 先对队列按照高到低的顺序排序,当高度相同时,多的在后面。这样从前往后挨个调整得时候,前面元素得移动只可能是往前诺,不会对后面的产生影响。后面的元素插入前面 也不会对已经插入过的影响,因为后面的身高低。
加油站
这道题使用 两个for循环遍历 也不会超时 时间复杂度是 O(N^2) 但是这样并不好。首先选一个 起点0运行 通过累加 油量 和 损耗量,到第 N 站如果 油量 > 损耗 说明无法到达,将起点修改为第N+1站作为新的开始 这里不是从0到1挨个 作为起点测试。因为,如果在第N站 油不够了 而前N站都够,那么油量>=消耗量,那么在这之中选择一个起点 油量=消耗=0 必然到第N站还是不够,所以起点直接选 N+1开始新的测试。
最低加油次数
当时看到这个题后 觉得和跳台阶有点像,但是其实底层逻辑完全不一样。跳台阶是 每个位置的数字代表能像前跳的最大步数,但是上一次的最大步数如果没用完,不能累加使用,可以在当前位置展望跳到下一个位置能够到达的最远距离。但是这个题目的油是可以累计的,因此再按照上面的贪心逻辑就不对了。
无重叠区间
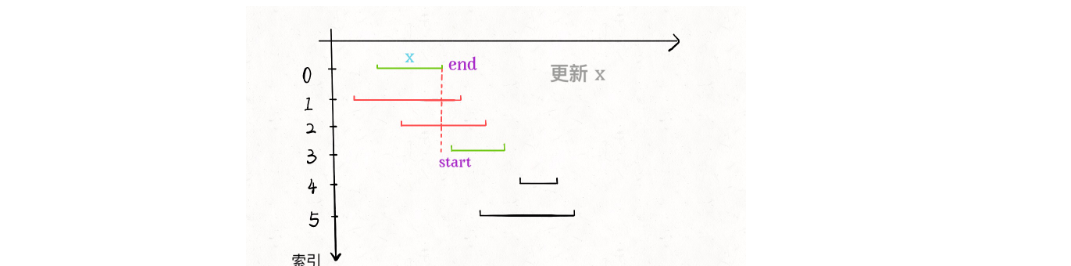
这个题和 用最少数量的箭引爆气球 题目类似。 首先 对区间的end位置 升序排列,如图所示,从上往下 依次寻找找没有交集且最邻近的 区间,直至结束。那么总数就是可以剩下的最大区间数。为何 这么做就是对的呢?考虑以下 例如从上往下 扫面的过程中, 第0个只和 第1,2 相交,那么 1,2相互也必定重叠。这三个必删掉 两个,删掉哪两个呢?若保留1或者2,那么不能保证 1或者2下面没有区间和它相交,但是保留1,则可以保证就没有其他的再可能与1相交。所以 应该删掉1,2.这也是一种贪心的思想。从上往下扫描,删掉与其相交的 区间。 但是按照上面思路去写代码 正确性有保证,但是并没有完全利用到里面的规律 会有冗余的 循环。 再接着 想,从上往下扫面,如果 遇到一个与其相交的 就跳过(代表删除了)再接着往下扫描直到遇到以一个与当前区间不相交的区间,此时将该区间的尾部坐标更新,再接着往下扫面。每次遇到不相交的区间计数加一 统计 总共不相交的区间数量即可。这样取第0个区间的时候 并没有依次遍历完下面所有与第0个区间相交的区间,但是任然可行。因为如果 x(0)(1) < x(3)(0) 即第0,3区间不相交 而 若 x(0)(1) > x(n)(0) 即 第 0 n区间也相交。那么x(3)(1) > x(3)(0) > x(n)(0) 即第3,n区间也必然相交。这样 即便在第0个区间的时候没扫描并删除第n个区间,但是在 切换到第三个区间并往下扫描的时候 也可以将n 删除。
划分字母区间
这个题的 关键就是 寻找 字母结束的最大位置,当 遍历到 第 i 个 字母时 i == end 则可以作为一个分割点
最大交换
在做题的时候 要首先理解清楚题目的意思,然后尽可能用简单的模型来描述 完成题目要求,而不是在边界情况都还想不清楚的时候,就下手用可能的方法解题。例如本题 一读题目就 感觉应该可以用单调栈写。其实本质就是求 高位 左边最大且 靠后 的数交换。用单调栈很难一下想到 且靠后 这种边界情况。
对于查找某个位置 一侧比他大的最大的最远/最近的数,像数字和字符,找它某一侧最大的数字的位置,可以不用
有效的括号字符串
这个题也可以使用两个栈做。但是贪心的方法更简单。对于不含有 星号 的问题,只需要累计左右括号的相对数量,如果始终是左括号数大于等于右括号数,并且最终左括号数等于右括号数,那么代表有效。如果有星号,当星号作为左括号时,左括号数可以为 x+1, 当它为右括号时,左括号数可以为 x - 1,所以当前位置的左括号数量累计为一个区间 [l_down, l_up] ,每次遇到 星号,l_down–,r_up++,当 l_down == 0 时,代表前面的左括号数最少为0个,此时再遇到星号,星号就不能再作为右括号了,因此 l_down 限制为0;当 左括号的最大上限 < 0 时,代表即便前面所有的星号都用做左括号,也无法保证左括号数大于等于右括号数。
最终如果最少的左括号数大于0,表明星号即便全作为右括号,也不够抵消所有的左括号,返回 false