记录了解题中双指针方法典型的题目,例如二分法中的首位指针,图的环判定中的快慢指针,滑窗方法等
双指针
二分查找
二分查找问题中,有的问题可以很明显套用二分查找的思路,例如有序数组等。但是有的问题比较隐晦,例如在 D 天内送达包裹的能力 最好的思路就是先按照暴力的方法找思路,如果了暴力可以做,再考虑是否可以二分优化,这种题的有序性就隐藏在了题的情景中,直接很难想到二分的思路。
旋转数组的最小数字
这个题有点意思。看题目很难朝二分查找上想。但凡是能用二分查找的就能用暴力。所以这个题如果先用暴力想到就可以简单的换成二分法。可以想到的是 船的运载量越大,越可能完成运载任务,题目要求可以完成运载任务的最小运载量。如果已经给定一个运载量,那么可以很容易地判断在这个运载量下能否完成运输。贪心地思想,每趟尽可能的多运,如果最后一天还运不玩 那说明这个运载量少了,需要增加运载量。于是暴力搜索运载量的方法就产生了。那么如何转换成二分呢。起始运载量越大越可能完成这个隐藏条件就是二分查找有序的条件。最后就是确定二分查找的边界。很明显当运载量为总重时是 右边界,运载量还得大于单个货物的重量。
这个题目和上面的题极为类似
分割数组的最大值
同上
乘法表中第k小的数
这个题套路和上面的题一样。但是这个难想一点,题目要求是求 K 大的元素,直观的想法是从1 … k 统计 乘法表中1的元素数量,2的元素数量,3的元素数量,然后就想着找规律了,然后没找出来。实际换个思路,可以很容易计算出 表中 小于等于 x 的个数,为什么呢?只需遍历所有的行,对于第 i 行 [1i, 2xi, 3xi,4xi…nxi],是个递增的,所以很容易知道该行小于 x 的元素个数 Min[x//i , n]。然后遍历所有行累加即可。知道了这个就可以 从 1 … nxm 遍历,判断表中 小于等于 x 的元素个数。x越大,表中小于他的元素就越多,由此可知 可以二分 。一共要搜索 log(mn)次,每次遍历表 m 行 时间复杂度为 O(mlogmn)
和上面那个题一样的思路。但是在判断查找结果能否满足要求时 不能遍历。
元素和小于等于阈值的正方形的最大边长
和上面的思路也是一样 只不过要用到前缀和 加速计算任意矩形面积元素和
直接能想到 根据归并中的思路,挨个合并。但是这样时间复杂度为 O(m + n) 题目要求复杂度为 O(log(m + n )) 这很明显要用二分搜索。有序的问题一般都能通过二分搜索解决。
有序数组中的单一元素
这个题要求时间复杂度为 O(logn) 则必须使用二分查找。这个题很有意思,给定数组中按照升序排列,找出单一的元素。这个题使用二分的关键在于 两个相同的元素相邻,根据 二分之后索引的奇数偶数来确定向前还是向后搜索。
寻找旋转排序数组中的最小值
二分法。这个题关键是找对比较对象,否则 特殊情况 不好处理。关键是 计算中值后都与右边的数比较 如果 mid > right 说明需要调整左区间++ 如果 mid < right 说明 mid 在右边,但是此时可能mid就是 最小值,所以 r = c; 而不减一。
在排序数组中查找元素的第一个和最后一个位置
寻找峰值
第一个难点在于如何将该问题转化为 二分查找的方法去做,另一个难点在 怎么用代码实现二分查找,写的不对的话 边界情况很麻烦,但是框架写对了,就不需要处理边界情况
滑动窗口
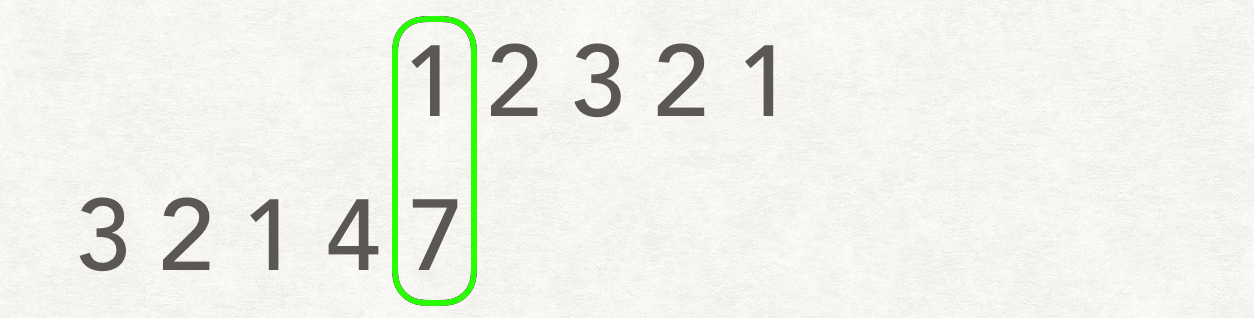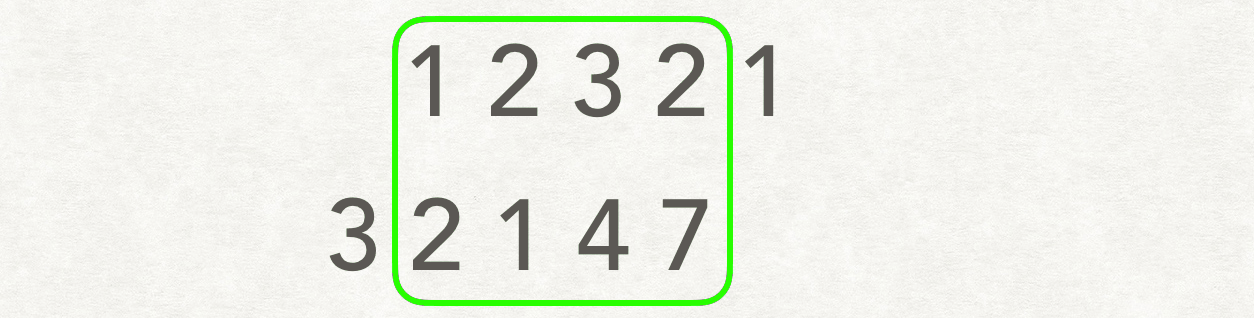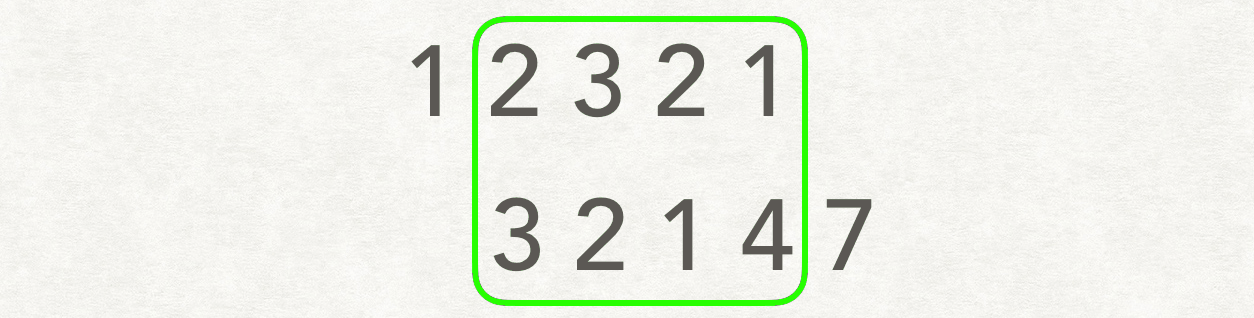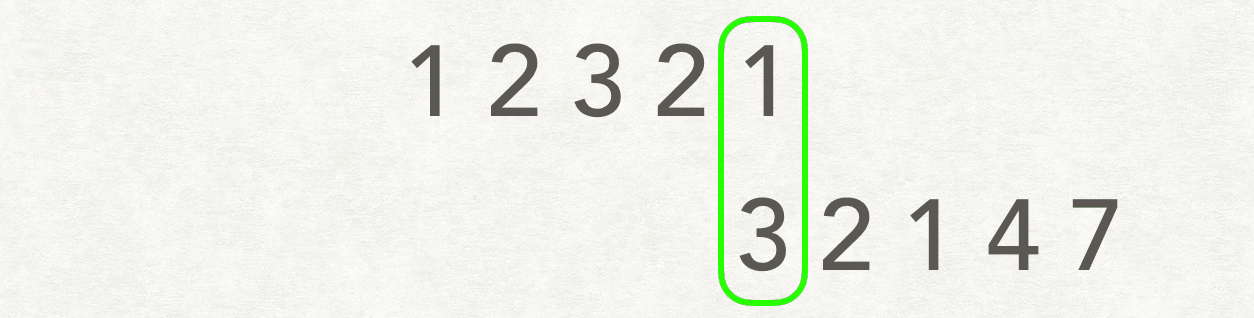
这个题 用 动态规划做复杂度 O(M x N)。滑动窗口解法复杂度 O((M + N) x min(M, N))
最小覆盖子串
这是个 很典型的 用滑动窗口的方法。右指针增加用于 扩大 窗口,当窗口中覆盖了需要的所有字符后,左指针不断收缩窗口。
找到字符串中所有字母异位词
这道题典型的使用双指针的方法来实现滑动窗口。初始两个指针都在起点,然后右指针滑动向右,和左指针构成一个滑窗。
首尾指针
和二分查找相同的是,这种题目也是根据有序的条件收缩 首位指针,去掉无用的搜索。因此对于简单的题目,可能题中有明显的有序的条件。但是有的比较隐晦。
盛最多水的容器
这是典型的双指针的题目。和二分法类似,但是二分查找有明显的排序条件在其中,总之都是根据一定的条件收缩指针。
其他
递增的三元子序列
有效三角形的个数
同样的 暴力 N^3 超时。因此可以通过手动排序的方法降低复杂度。排序一下子就想到了 但是没想到优化,排序后自然而然就要想到双指针优化,使得复杂度降低为 N^2 ,固定一个最大的边,然后使用双指针去搜索另外两个小的边
最小区间
这个题可以看作一个典型的多指针解决的问题。有多个递增的序列 首先就应该想到双指针 二分之类的思路。我当时就是想到了二分法,以一个数组为基准遍历里面的每个元素,然后去其他数组中搜索离它最近的元素,这样每个数组都能找到一个最近的,将这几个最近的合并成完整的区间即可。但是这样是错的,因为最近的元素可能会有左右两个 例如 4 9 中搜索5,离他最近的是4,但是就一定是选4嘛?不一定,因为还要看其他区间,也有可能选9,所以要考虑左右相邻的合并问题,没有想到很好的解决方法
标准答案是 使用多指针。由于需要在每个数组中都找一个对应的,那么就都取数组的第一个,一共K个元素使用小顶堆维护,并找到最大值,最小值到最大值即为一个区间。然后就是指针的移动条件,每次移动小顶堆中最小的那个指针。即一个区间头指针一个尾指针,数组递增,移动头指针肯定越移动区间长度越大,所以只能移动尾指针。如此动态更新。
另一个解法应该想到的。换个思路,将数组中的元素看作 a b c…. 的编号,然后将所有数组依序合并成一个新的递增序列 然后使用滑窗 保证窗中至少覆盖一个 a b c 即可。就转换为最小覆盖子串的问题了。