同态滤波
基本原理
同态变换一般是指将非线性组合信号通过某种变换,使其变成线性组合信号,从而可以更方便的运用线性操作对信号进行处理。
所谓非线性组合信号,举例来说,比如 z(t) = x(t) y(t),两个信号相乘得到组合信号,由于时域相乘等价于频率域卷积,所以无法在频率域将其分开。但是我们应用一个log算子,对两边取对数,则有: log(z(t)) = log(x(t)) + log(y(t)),这样一来,就变成了线性组合的信号,log(x(t)) 和 log(y(t)) 时域相加,所以频域也是相加的关系,如果它们的频谱位置不同,就可以傅里叶变换后较好的分开,以便进行后续的分别的操作,比如应用高、低通滤波或者其他手工设计的滤波器等,然后再将结果傅里叶反变换,得到处理过的 ,在取幂,就可以得到最终的处理结果。
图像中的同态滤波
在图像处理中,常常遇到动态范围很大但是暗区的细节又不清楚的现象,我们希望增强暗区细节的同时不损失亮区细节,一般来说,我们可以将图像f(x,y)建模成 照射强度(illumination) i(x,y) 和 反射强度(reflection) r(x,y)的乘积,所以有:

一般来说,自然图片的光照一般是均匀渐变的,所以i应该是低频分量,而不同物体对光的反射是具有突变的,所以r是高频分量。现在我们对两边取对数,并做Fourier变换,得到线性组合的频率域。

我们希望对低频能量进行压制(抑制掉 光照分量),这样就降低了动态范围,而要对高频进行提高,这样就增强了图像的对比度,示意图如下:

所以采用的滤波器为:

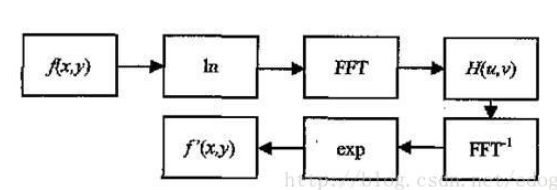
操作完成后在按照之前介绍的步骤,反变换,求幂,即可得到处理后的图像,整个过程的流程图如下: