MSR-NET

Retinex 系列算法

Retinex原理

I(x) = R(x) · L(x) 对上式子取对数，得到 Log[R(x,y)] = Log[I(x,y)] - Log[L(x,y)] = Log[R(x,y)] = Log[I(x,y)] - Log[I(x,y)*F(x,y)] ( *表示卷积)
把这个技术运用到图像处理上，就是针对我们现在已经获得的一副图像数据I(x,y），计算出对应的R(x,y)，则R(x,y)认为是增强后的图像，现在的关键是如何得到L(X,Y)。Retinex理论的提出者指出这个L(x,y）可以通过对图像数据I(x,y）进行F(x,y)高斯模糊而得到，从实际运用的角度来说，也可以用均值模糊来代替高斯模糊。

输入：原始图像数据I(x,y),尺度（也就是所谓的模糊的半径）
处理：
- 计算原始图像按指定尺度进行模糊后的图像 L(x,y);
- 按照上式的计算方法计算出 Log[R(x,y)]的值
- 将 Log[R(x,y)]量化为0到255范围的像素值，作为最终的输出

上述在讲Log[] 量化时，会产生色彩失真。这也是这算法的通病。上述实现的算法通常叫SSR (Single Scale Retinex,单尺度视网膜增强）

MSR (Multi-Scale Retinex)

最为经典的就是3尺度的，大、中、小，既能实现图像动态范围的压缩，又能保持色感的一致性较好。同单尺度相比，该算法有在计算Log[R(x,y)]的值时步骤有所不同。

需要对原始图像进行每个尺度的高斯模糊，得到模糊后的图像Li(x,y),其中小标i表示尺度数
对每个尺度下进行累加计算 Log[R(x,y)] = Log[R(x,y)] + Weight(i)* ( Log[Ii(x,y)]-Log[Li(x,y)]); 其中Weight(i)表示每个尺度对应的权重，要求各尺度权重之和必须为1，经典的取值为等权重

带色彩恢复的多尺度视网膜增强算法(MSRCR,Multi-Scale Retinex with Color Restoration)

其改进在于对Log量化过程的改进：

分别计算出 Log[R(x,y)]中R/G/B各通道数据的均值Mean和均方差Var（注意是均方差）
利用类似下述公式计算各通道的Min和Max值 Min = Mean - Dynamic * Var; Max = Mean + Dynamic * Var;
对Log[R(x,y)]的每一个值Value，进行线性映射：

R(x,y) = ( Value - Min ) / (Max - Min) * (255-0)

同时要注意增加一个溢出判断,即：

if (R(x,y) > 255) R(x,y) =255; else if (R(x,y) < 0) R(x,y)=0

more...

参考链接： https://www.cnblogs.com/Imageshop/archive/2013/04/17/3026881.html https://cloud.tencent.com/developer/article/1011768

MSR-net

### 主要贡献：

作者认为传统的MSR多尺度视网膜增强算法的过程可以用神经网络去模拟，并且神经网络的参数可以根据数据自学习。相对传统的采用固定的高斯模糊核要灵活 多尺度Retinex实际上相当于一个具有残差结构的前馈卷积神经网络
提出MSR-net 基于Retinex模型和神经网络的方法端到端得学习亮暗图之间得映射

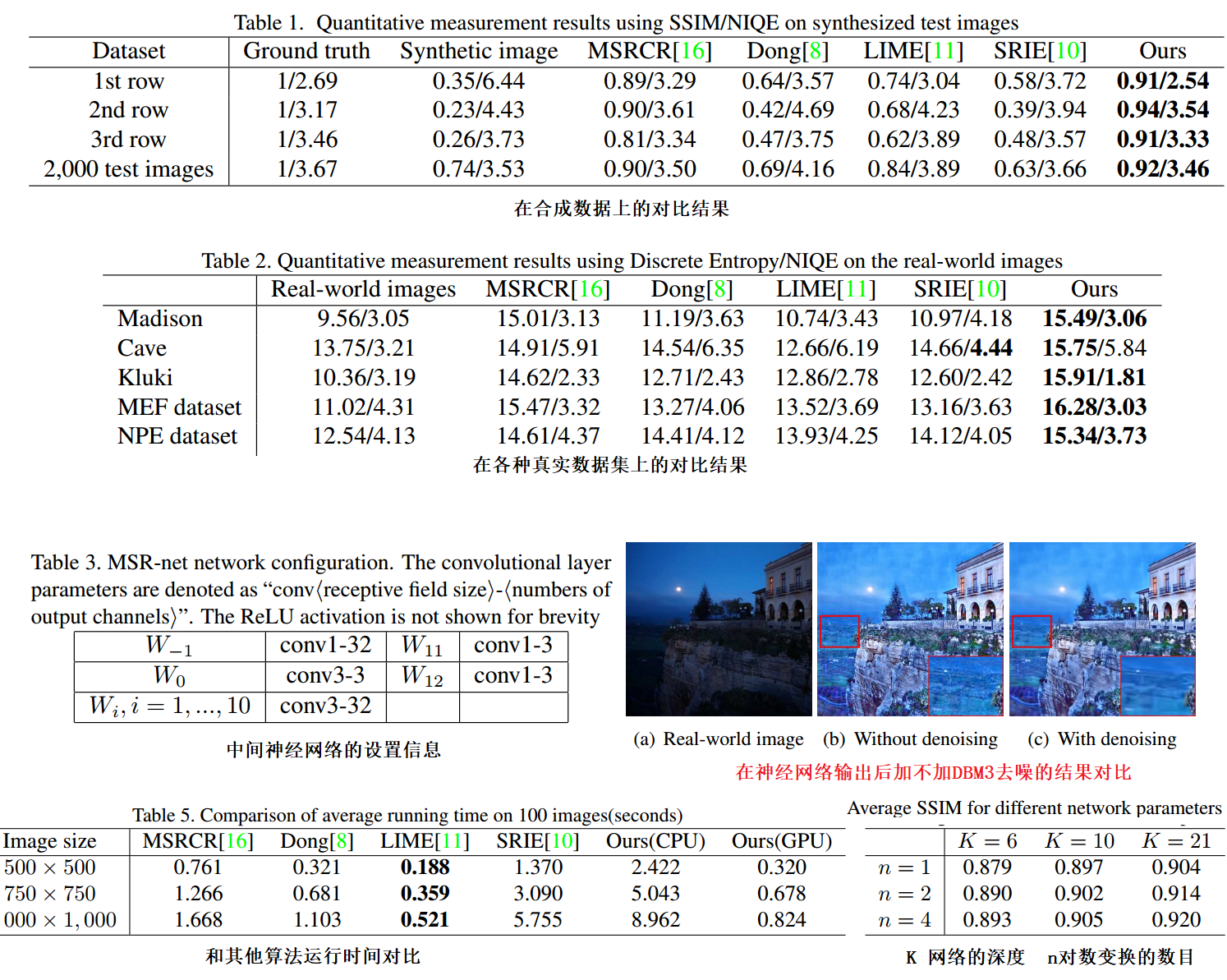
结构图

多尺度对数变换f1

\[ M_{j}=\log _{v_{j}+1}\left(1+v_{j} \cdot X\right), j=1,2, \ldots, n \]

输入的一幅3通道的图像，经过对数变换为 n*3 通道的tensor。 log函数具有压缩高灰度值的数据，拉伸低灰度值的数据。X代表输入图像，vj代表对应的尺度n代表尺度数。接着，使用一个卷积+Relu 。上述的操作主要是通过多次对数变换的加权和来得到更好的图像，加速了网络的收敛。

Difference-of-convolution f2

这里的卷积代表着对不同尺度的图像进行平滑处理。将不同卷积层的输出contact 一起最后来个1X1卷积，相当于MSR中对不同尺度的SSR输出的加权平均。1X1之后引入了一个 “-” 操作，与SSR中的 Log[I(x,y)] - Log[L(x,y)] 减的目的相同，根据模拟产生的L(x,y) 还原出Log[R(x,y)] 深度为K

颜色重建函数 f3

由于上一步减的到的是 Log(R(x,y)) 因此最后一个1X1卷积就是用来色彩还原的。上述三步的输出结果可视化如下：

损失函数

\[ L=\frac{1}{N} \sum_{i=1}^{N}\left\|f\left(X_{i}\right)-Y_{i}\right\|_{F}^{2}+\lambda \sum_{i=-1}^{K+2}\left\|W_{i}\right\|_{F}^{2} \]

实验

数据集

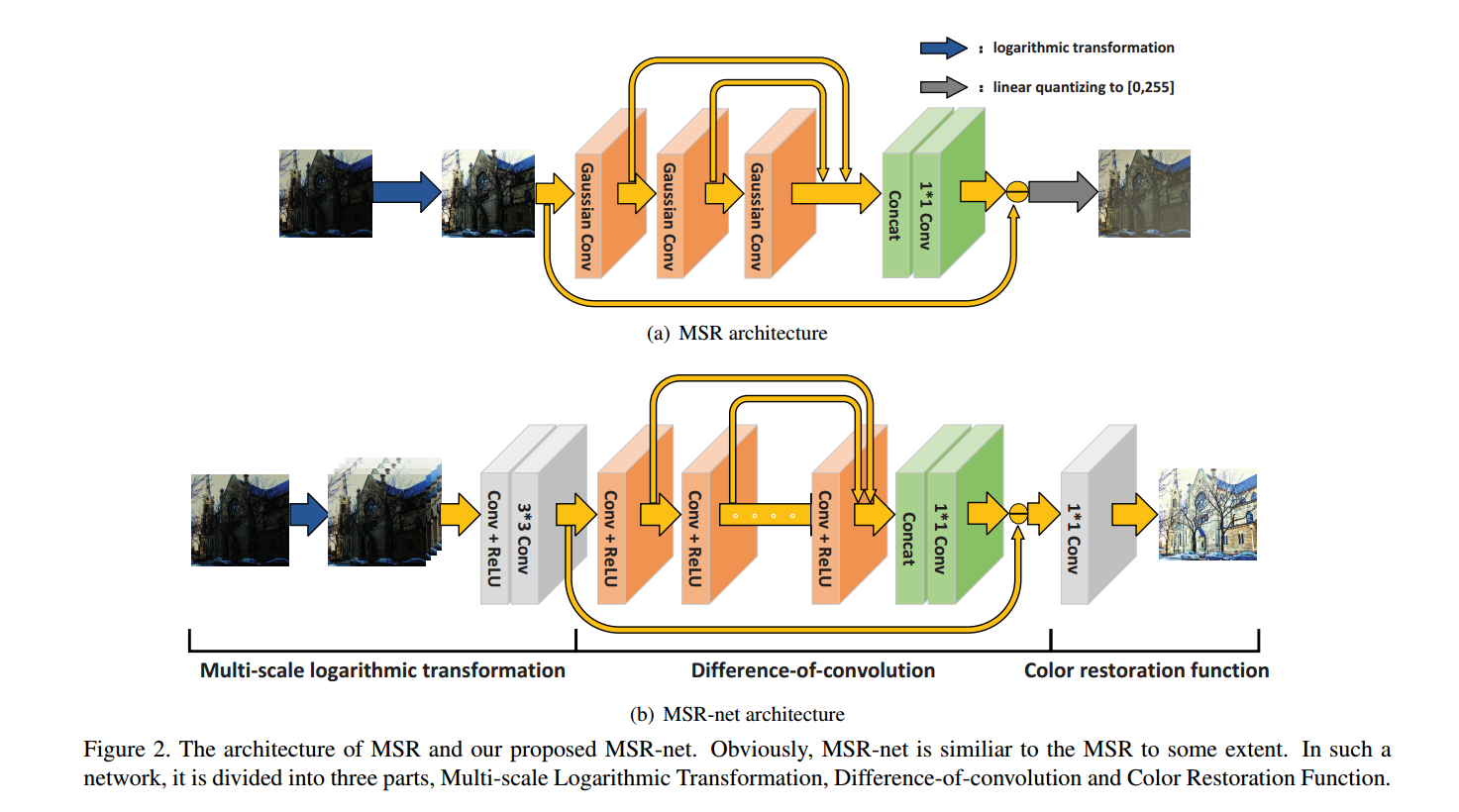
依然是同时使用合成图像验证，使用公开的真实的数据集。同时还对比了各种超参数对结果的影响。作者建立了一个新的真实数据集包含HQ LQ图片 同时还使用了已有的正式低光照数据集 MEF NPE VV

训练参数

中间的神经网络的深度为K ， adam 权重衰减为10-6 batch_size为64 初始学习率为10-4 学习率除10每100K到200K iteration。作者实验发现带有第一个对数多尺度变换的要比单尺度变换的效果好 4个变换尺度，分别为1，10，100，300

Ruowang's blogs

MSR