Zero-Reference Deep Curve Estimation for Low-Light Image Enhancement
主要贡献
- 提出了第一个不依赖于成对训练图像的低光照图像增强卷积神经网络
- 设计了一个 可以近似像素映射的 image-specific 曲线以及通过迭代方式形成的高阶曲线。这种特定于图像的曲线可以在很大的动态范围内有效地执行像素映射。
- 在没有参考图像的情况下,通过设计 特定的 任务相关的损失函数来训练深度网络 这种方法存在巨大的潜力。
- 640 x 480输入图像 500 FPS
主要方法
光照增强曲线 LE-curve
作者说受 P图软件的 曲线调整的启发,有了这个思想。希望设计一个 可以自动增强图像的曲线,其中自适应曲线参数仅依赖于输入图像。这种曲线的设计要有如下性质:
- 增强后图像的每个像素值都应在归一化范围[0,1]内,以避免溢出截断导致的信息丢失;
- 曲线应该是单调递增的,以保持相邻像素的差异(对比度); 就是本来输入低光照图像较亮的区域输出对应也应该更亮,而不是反而变暗。
- 这种曲线可微,可以反向传播。
从上述需要的三个条件可以看出,作者设计的这种曲线感觉和 图像直方图调整的那个曲线不是一回事。这个曲线就是一个对输入图像的像素经过一个非线性映射然后输出吧,类似gamma的增强方法?所以这个曲线得满足单调可谓等的性质,与gamma不同的是,这个曲线参数由CNN输出,其不同像素位置的曲线参数不同,而gamma是全局用一条曲(但是文中这么设计我觉得仅仅是曲线是单调递增得并不能保证相邻像素输出得对比度差异,因为相邻像素使用得曲线参数不一样,虽然两条曲线都是递增得,但是分别对应映射输出后得值不一定依旧保证输入之前的相对大小关系,可能这种情况通过后面的损失函数,网络训练完之后便不会出现了吧),换句话说就是不同像素位置的 映射方式不同。具体设计的曲线 如下式子:
\[L E(I(\mathbf{x}) ; \alpha)=I(\mathbf{x})+\alpha I(\mathbf{x})(1-I(\mathbf{x}))\]
上式中 \(I(\mathbf{x})\) 为输入图像的x位置的像素值,\(\alpha\)为曲线调整的参数,由CNN输出决定,不同的\(\alpha\)对应不同形状的曲线参数,具体可见下图。例如当\(\alpha\)=-1时,就是一个二次曲线,输入输出的映射关系为二次关系。同理。 同时将上式迭代,可以构成更高阶的曲线。
\[L E(I(\mathbf{x}) ; \alpha)=I(\mathbf{x})+\alpha I(\mathbf{x})(1-I(\mathbf{x}))\]
最后,每个像素位置的\(\alpha\)参数都不同,也就是不同位置的 曲线映射方式不一样,所以CNN输出的\(\alpha\)其实是和输入图像大小一样的。而由于有n次迭代,每次迭代分别对 RGB 三通道使用独立的\(\alpha\) 所以最终CNN输出的feature map的尺寸应该是n x 3 x W x H大小的。如下图:
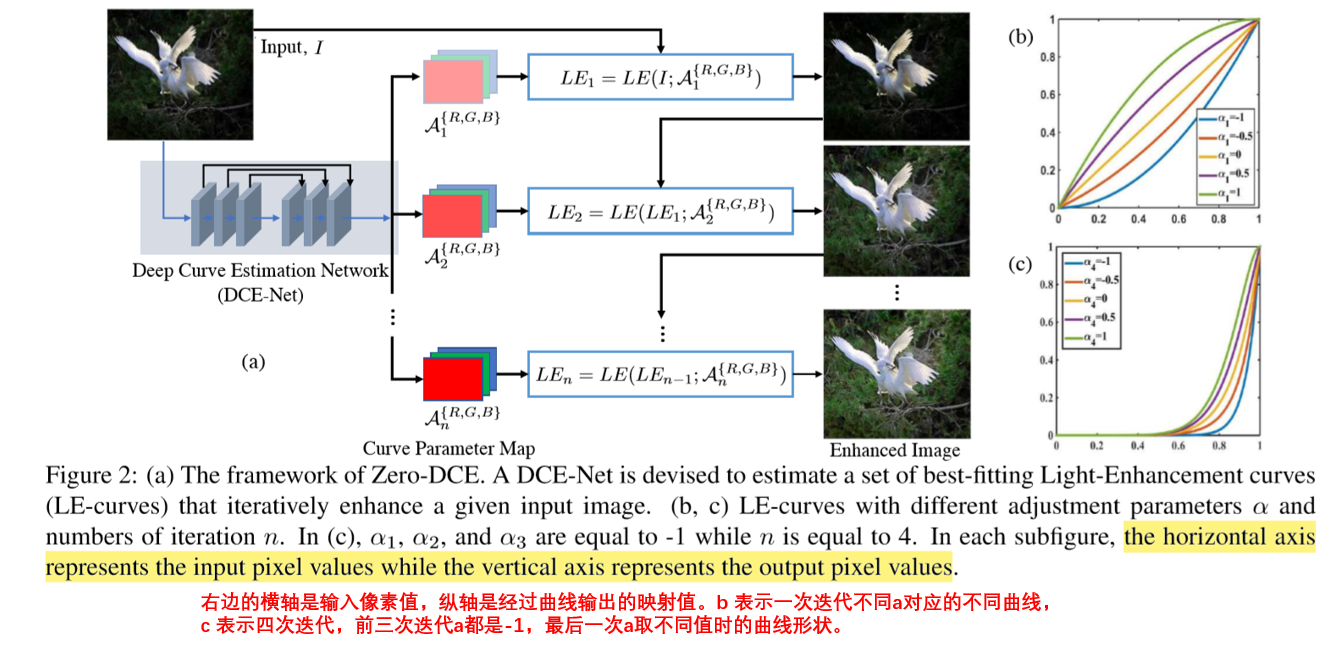
上图 b 可以看出:
- 对于迭代一次的曲线,当\(\alpha = -1\) 为二次曲线,即输入x > 输出y; 这种情况对于过曝的像素可以压缩它的像素值。
- ... 当\(\alpha = 0\) 为恒等映射,输入输出不变
- ... 当\(\alpha = 1\)时,曲线为凸函数,即 输入x < 输出y; 这种情况可以增大像素值,对应光照增强。
因此这种曲线调整的方式 不仅有可以增强低曝光区域像素的能力,还可以压缩过曝区域的像素。
DEC-Net
就是常规的CNN,主要是轻量。他的输出特征为A,通道数为迭代次数x3(RGB),尺寸和输入图像一样。
损失函数 Non-Reference Loss Functions
我觉得这就是最关键的地方吧,感觉前面说的曲线的方式 和 传统的CNN学习端到端的像素映射没什么区别,不能决定它不用参考图像来训练。
- 可能 增加 a 的曲线方式可以增强 CNN的非线性性?可以试试去掉后面的曲线调整部分,直接CNN输出增强后的图像,然后用这个损失函数来做看效果。
空间一致性损失 Spatial Consistency Loss
\[L_{s p a}=\frac{1}{K} \sum_{i=1}^{K} \sum_{j \in \Omega(i)}\left(\left|\left(Y_{i}-Y_{j}\right)\right|-\left|\left(I_{i}-I_{j}\right)\right|\right)^{2}\]
作者描述的这个损失的目的是,保留输入图像和输出图像对应位置像素和相邻像素之间的差异。其中K表示局部区域像素数,\(\Omega(i)\)是像素位置\(i\)的上下左右四个领域位置。\(Y,I\) 分别表示增强后的图像和输入图像。感觉这个式子和局部梯度相似性很像。
曝光控制 Exposure Control Loss
为了抑制过曝和欠曝的出现,用这个损失函数来控制图像整体曝光水平。这项就是衡量局部区域(16x16)的像素值的平均水平与 常数E例如0.6之间的差距。作者说这个E取[0.4, 0.7]差别不大。
\[L_{e x p}=\frac{1}{M} \sum_{k=1}^{M}\left|Y_{k}-E\right|\]
颜色恒常损失Color Constancy Loss
基于 Gray-World color constancy hypothesis 这个规则,对于一幅有着大量色彩变化的图像,R,G,B, 三个分量的平均值趋于同一灰度值。 从物理意义上讲,灰色世界法假设自然界景物对于光线的平均反射的均值在总体上是个定值,这个定值近似地为“灰色”。也就是一个正常的彩色图像,R,G,B三通道的平均值应该都相等。避免
\[L_{c o l}=\sum_{\forall(p, q) \in \varepsilon}\left(J^{p}-J^{q}\right)^{2}, \varepsilon=\{(R, G),(R, B),(G, B)\}\]
上式含义显而易见。设计了色彩恒常性损失,以纠正在增强的过程中可能出现的颜色偏差。
光照平滑 Illumination Smoothness Loss
这个损失就 类似 Retinex中的局部光照一致性原理。即局部区域的 a 参数应该是一样的。
实验
使用SICE数据集中的 2422张训练,其余的测试。 每张图resize到512x512进行训练。
各项损失函数的作用
作者分别去掉四项损失中的一项,进行训练得到的结果如下:

- 去掉 spa损失,对比度细节下降,如空中的白云。
- 去掉 esp损失,图像暗区域的曝光度降低,没能成功增强暗区域
- 去掉 col 颜色恒常损失,可以看出图片整体颜色出现偏色
- 没有 tv 光照平滑损失,图像出现严重伪影
各项参数的影响

网络深度-通道数-迭代次数。可以看出对比def三个图,可以看出 迭代一次的曲线增强能力太弱,因此需要更多次的迭代来合成高阶曲线,这样曲线具有更强的调整能力。
训练数据的影响
作者 做了三类训练数据
- 原本DEC训练数据中的一部分900张 只有欠曝光的图像。DEC_low
- DARK FACE数据集中收集的 9000张 低光照数据集,也是只有低光照数据集。DEC_large_L
- 使用数据增广的方法,包含了 过曝光和欠曝光图像,从1,2部分获得的数据集 4800张 DEC_large_LH

由图c,d可以看出,如果训练数据中不含有过曝光数据,最终网络会对原本光照正常的区域造成过曝光,但是如果低光照数据多,对暗区域增强的能力要强。因此
- 训练数据集中必须有 过曝光图像,防止过曝
- 低光照训练图像多的话,网络的增强能力要强。
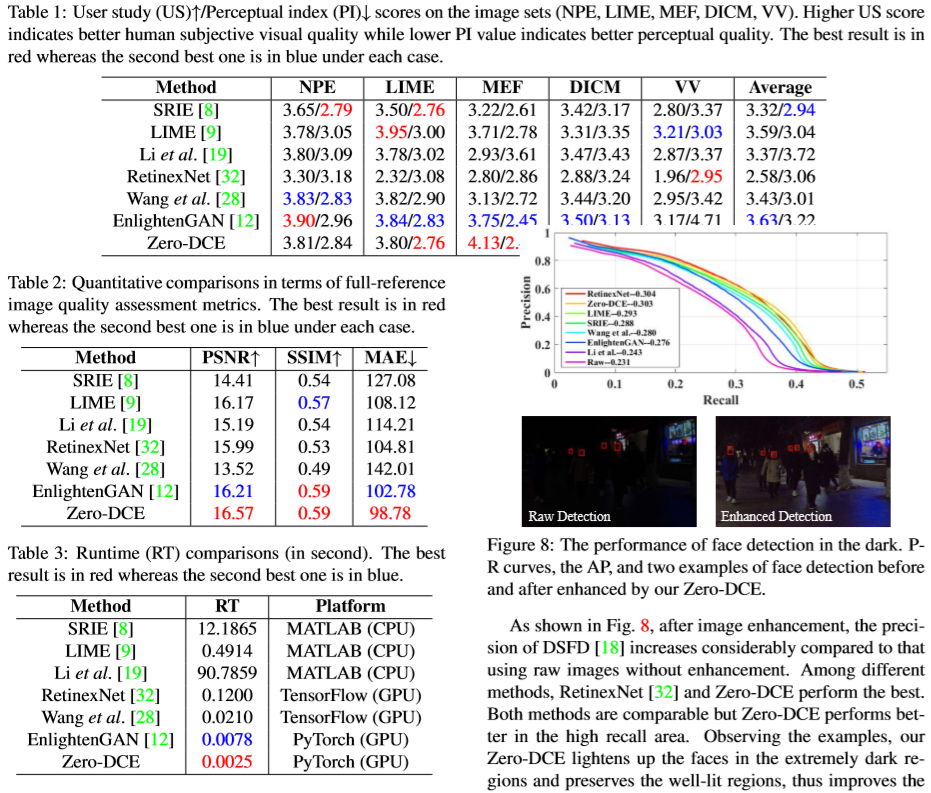
最终对比结果